Laboratorio virtuale > Rosso e nero > 1 2 [3] 4 5

3. Gioco aggressivo

Ricordiamo che, nel caso di gioco aggressivo, il giocatore punta a ciascuna prova la sua intera ricchezza o, se è minore, la quantità di denaro necessaria per raggiungere la ricchezza obiettivo. Siamo interessati alla probabilità che il giocatore raggiunga l'obiettivo e al numero atteso di prove. Il primo fatto interessante è che solo il rapporto tra ricchezza iniziale e ricchezza obiettivo è rilevante, al contrario di quanto accade nel caso di gioco prudente.

1. Supponi che il giocatore giochi aggressivamente con una ricchezza iniziale pari a x e una ricchezza obiettivo a. Dimostra che, per ogni c > 0, il processo cX_i, i = 0, 1, 2, ... è il processo della ricchezza per il gioco aggressivo con ricchezza iniziale cx e ricchezza obiettivo ca.

Grazie al risultato dell'esercizio 1, conviene utilizzare la ricchezza obiettivo come unità monetaria e permettere di avere ricchezze iniziali sia razionali che irrazionali. Lo spazio delle ricchezze è quindi [0, 1].

Probabilità di vincita

Indicheremo la probabilità che il giocatore raggiunga a = 1 partendo da x in [0, 1] con F(x). Per l'esercizio 1, la probabilità che il giocatore raggiunga un altro valore qualsiaasi a, partendo da x in [0, a], è F(x/a).

2. Condizionando all'esito della prima prova, mostra che F soddisfa l'equazione funzionale

F(x) = pF(2x) per x in [0, 1 / 2], F(x) = p + qF(2x - 1) per x in [1 / 2, 1]

e che F soddisfa le condizioni di limite F(0) = 0, F(1) = 1.

Espansioni binarie

Il fulcro della nostra analisi sarà la rappresentazione in forma binaria della ricchezza iniziale. L'espansione binaria di x in [0, 1) è

x = u₁ / 2 + u₂ / 2² + u₃ / 2³ + ···

dove u_i appartiene a {0, 1} per ogni i. Tale rappresentazione è unica a parte il caso in cui x è un razionale binario della forma

x = k / 2ⁿ dove n = 1, 2, ... e k = 1, 2, ... 2ⁿ - 1.

Il più piccolo valore possibile di n in questa rappresentazione (dopo aver semplificato), è detto rango di x. Per un razionale binario x di rango n, useremo la rappresentazione standard, dove

u_n = 1 e u_i = 0 per i > n.

Il rango può essere esteso a tutti i numeri in [0, 1) ponendo a 0 il rango di 0 (0 è considerato anche un binario razionale) e ponendo a infinito il rango di un irrazionale.

Definiamo quindi le seguenti funzioni di x in [0, 1):

• u_i(x) = i-esima coordinata nell'espansione binaria di x
• z_i(x) = k - [u₀(x) + u₁(x) + ··· + u_k(x)] = numero di zeri nelle prime k cifre binarie.
• n(x) = rango di x.

3. Prova che

u_i(2x) = u_{i +} 1(x) se x in (0, 1 / 2), u_i(2x - 1) = u_{i +} 1(x) se x in [1 / 2, 0)

La probabilità di vincita vista da un'altra angolazione

4. Supponi che il giocatore parta con una ricchezza pari a x in (0, 1). Mostra che il giocatore prima o poi raggiunge l'obiettivo 1 se e solo se esiste un intero positivo k tale che

I_j = 1 - u_j(x) per j = 1, 2, ..., k - 1 e I_k = u_k(x).

Introduciamo ora un'interessante variabile casuale che ricopre un ruolo fondamentale nella nostra analisi. Sia

W = _{j = 1, 2, ...} (1 - I_j) / 2^j.

Notiamo che W è una variabile casuale ben definita e assume valori in [0, 1].

5. Supponi che il giocatore parta con una ricchezza pari a x in (0, 1). Usa il risultato dell'esercizio 4 per provare che il giocatore raggiunge l'obiettivo 1 se e solo se W < x.

6. Prova che W ha distribuzione continua. Ovvero, mostra che P(W = x) = 0 per ogni x in [0, 1].

Segue, dai risultati degli esercizi 5 e 6, che F è semplicemente la funzione di ripartizione di W. In particolare, F è una funzione crescente, e poiché W è continua, F è funzione continua.

Per gli esercizi 7–10 seguenti, sia

x = k / 2^m dove m appartiene a {1, 2, ...}, k appartiene a {0, 1, ... 2^m - 1} e y = (k + 1) / 2^m.

7. Prova che o x o y ha rango m.

8. Dimostra che l'unica sequenza di esiti che provocano la rovina del giocatore quando la ricchezza iniziale è x e la vittoria quando la ricchezza iniziale è y è la sequenza

I_j = u_j(x) - 1 per j = 1, 2, ..., m.

9. Usa il risultato dell'esercizio 8 per mostrare che

F(y) = F(x) + p^zm(x) q^{m - zm(x)}.

10. Prova che

F(x) = {p^zm(t) q^{m - zm(t)}: t < x, n(t) m}.

11. Mostra che

F(1 / 8) = p³, F(2 / 8) = p², F(3 / 8) = p² + p²q, F(4 / 8) = p

F(5 / 8) = p + p²q, F(6 / 8) = p + pq, F(7 / 8) = p + pq + pq²

12. Usa il risultato dell'esercizio 9 per mostrare che F è strettamente crescente su [0, 1]. Ciò significa che la distribuzione di W ha supporto [0, 1]; ovvero non esistono sottointervalli di [0, 1] con lunghezza positiva e probabilità 0.

13. Usa l'induzione sul rango per mostrare che due soluzioni qualsiasi dell'equazione funzionale dell'esercizio 2 devono concordare sui binari razionali. Pertanto, ogni soluzione dell'equazione funzionale dell'esercizio 2 deve soddisfare i risultati degli esercizi 9 e 10.

14. Usa il risultato dell'esercizio 13 per mostrare che F è l'unica soluzione continua all'equazione funzionale dell'esercizio 2.

15. Supponi che p = 1 / 2. Mostra che F(x) = x soddisfa l'equazione funzionale dell'esercizio 2.

Nel caso di prove equilibrate, quindi, la probabilità che il giocatore aggressivo raggiunga a partendo da x è x/a, cioè quanto per il giocatore prudente.

Notiamo dall'esercizio 15 che, se p = 1 / 2, W ha distribuzione uniforme su [0, 1]. Se p è diverso da 1/2, la distribuzione di W è un po' strana. Per esprimere il risultato in forma compatta, indicheremo la dipendenza della misura di probabilità P dal parametro p. Definiamo

C_p = {x (0, 1): z_k(x) / k p per k }.

ovvero l'insieme degli x in (0, 1) per cui la frequenza relativa di zeri nell'espansione binaria è p.

16. Usa la legge forte dei grandi numeri per mostrare che

1. P_p(W C_p) = 1
2. P_p(W C_t) = 0 per t p.

Segue dall'esercizio 16 che, quando p è diverso da 1/2, W non ha densità, pur essendo una variabile casuale continua. La dimostrazione che ne diamo è per assurdo: se W avesse densità f allora

1 = P_p(W C_p) = _Cp f(x)dx = 0.

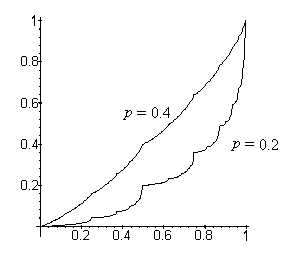
poiché lunghezza(C_p) = P_1/2(W C_p) = 0. Ciò significa che, quando p è diverso da 1/2, F ha derivata 0 in quasi ogni punto dell'intervallo [0, 1]. L'immagine seguente riporta i grafici di F per p = 0.2 e 0.4.

17. Nell'esperimento del rosso e nero, seleziona gioco aggressivo. Modifica x, a e p con le barre a scorrimento e osserva come cambia la distribuzione della ricchezza finale. In particolare, nota che la distribuzione della vincita dipende solo da x / a. Con a = 64, x = 24 e p = 0.45, simula 1000 replicazioni, aggiornando ogni 100, e osserva la convergenza delle frequenze relative alla funzione di densità.

Numero atteso di prove

Definiamo

G(x) = E(N | X₀ = x) per x in [0, 1].

Per ogni altro valore di a, e ogni x appartenente a [0, a], il numero atteso di prove è semplicemente G(x / a).

18. Condizionando all'esito della prima prova, mostra che G soddisfa l'equazione funzionale

G(x) = 1 + pG(2x) per x in (0, 1 / 2], G(x) = 1 + qG(2x - 1) per x in [1 / 2, 1)

e che G soddisfa le condizioni di limite G(0) = 0, G(1) = 0.

È interessante notare che l'equazione funzionale non è soddisfatta in x = 0 o x= 1. Come in precedenza, la rappresentazione binaria della ricchezza iniziale x in (0, 1) è fondamentale per la nostra analisi.

19. Supponi che la ricchezza iniziale del giocatore sia un binario razionale x in (0, 1). Prova che

N = min{k = 1, 2, ...: I_k = u_k(x) o k = n(x)}.

Per cui i possibili valori di N sono 1, 2, ..., n(x).

20. Supponi che la ricchezza iniziale sia un binario irrazionale x in (0, 1). Mostra che

N = min{k = 1, 2, ...: I_k = u_k(x)}.

Per cui i valori possibili di N sono 1, 2, ....

Possiamo trovare una formula esplicita per il numero atteso di prove G(x) in termini della rappresentazione binaria di x.

21. Supponi che x in (0, 1) sia un binario razionale. Prova che

G(x) = 1 + _{i = 1, ..., n(x) - 1} p^zi(x) q^{i - zi(x)}.

22. Usa il risultato dell'esercizio precedente per mostrare che

G(1 / 8) = 1 + p + p², G(2 / 8) = 1 + p, G(3 / 8) = 1 + p + pq, G(4 / 8) = 1

G(5 / 8) = 1 + q + pq, G(6 / 8) = 1 + q, G(7 / 8) = 1 + q + q²

23. Supponi che x in (0, 1) sia un binario razionale. Mostra che

G(x) = 1 + _{i = 1, 2, ...} p^zi(x) q^{i - zi(x)}.

24. Supponi che p = 1 / 2. Prova che

1. G(x) = 2 - 1 / 2^{n(x) - 1} se x è un binario razionale
2. G(x) = 2 se x è un binario irrazionale

25. Nell'esperimento del rosso e nero, seleziona gioco aggressivo. Modifica x, a e p con le barre a scorrimento e osserva come cambia il numero atteso di prove. In particolare, nota che la media dipende solo da x / a. Con a = 64, x = 24 e p = 0.5, simula 1000 replicazioni, aggiornando ogni 100, e osserva la convergenza delle media campionaria al valore atteso.

26. Per dato x, prova che G è continua in funzione di p.

In funzione della ricchezza iniziale x e per dato p, la funzione G è molto irregolare. In realtà G è discontinua per i binari razionali dell'intervallo [0,1] e continua negli altri punti. Gli esercizi seguenti ne danno la dimostrazione.

27. Prova che, per b > 0, esiste un M tale che, per ogni x

_{i = M, ...} p^zi(x) q^{i - zi(x)} < b.

28. Supponi che x in (0, 1) sia un binario irrazionale. Per l'M dell'esercizio 10 esiste un intervallo binario di rango M che contiene x:

k / 2^M < x < (k + 1) / 2^M.

Mostra che, se y appartiene a tale intervallo, allora x e y hanno le stesse cifre binarie, fino all'ordine M - 1, per cui

|G(y) - G(x)| < b.

29. Supponi che x sia un binario razionale di rango n. Per m = 1, 2, ... definisci y_m come

u_i(y_m) = u_i(x) per i = 1, 2, ..., n; u_i(y_m) = 1 per i = n + m; u_i(y_m) = 0 altrimenti.

Dimostra che y_m converge a x al crescere di m, ma che

G(x) < G(y₁) < G(y₂) < ···

Laboratorio virtuale > Rosso e nero > 1 2 [3] 4 5
Sommario | Applets | Dati | Biografie | Risorse | Indice analitico | ©