1. Usa la
regola del prodotto del calcolo combinatorio per mostrare che
Laboratorio virtuale > Modelli di campionamento finito > 1 2 3 4 5 6 [7] 8 9 10
Analogamente al modello di campionamento semplice, supponiamo di selezionare n numeri a caso, con reinserimento, dalla popolazione D = {1, 2, ..., N}:
X = (X1, X2, ..., Xn).
Ricordiamo che l'assunzione di base è che X sia distribuita uniformemente su
S = {1, 2, ..., N}n.
Il problema del compleanno consiste nel calcolare la probabilità dell'evento che ci sia almeno un valore doppio nel campione:
BN, n = {Xi = Xj per almeno una coppia distinta di indici i, j}.
Supponi di scegliere a caso n persone e registrare i loro compleanni. Se ignoriamo gli anni bisestili e assumiamo che i compleanni siano distribuiti uniformemente sull'anno, allora possiamo applicare il modello di campionamento con N = 365. In questo contesto, il problema del compleanno consiste nel calcolare la probabilità che almeno due persone abbiano lo stesso compleanno (di qui il nome del problema).
La soluzione generale al problema del compleanno è un semplice esercizio di calcolo combinatorio.
1. Usa la
regola del prodotto del calcolo combinatorio per mostrare che
N.Suggerimento: L'evento complementare si verifica se e solo se il vettore degli esiti X forma una permutazione di dimensione n da {1, 2, ..., N}
Il fatto che la probabilità sia 1 per n > N è detto a volte principio della piccionaia: se più di N piccioni si posizionano in N caselle, allora almeno una casella ospita più di un piccione.
2. Sia N =
365 (problema del compleanno standard). Mostra che la probabilità è
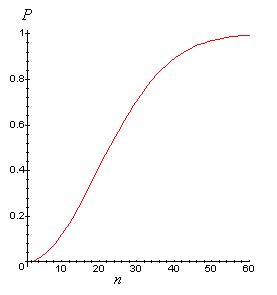
3. Disegna il grafico dei valori dell'esercizio 2 in funzione di n. Se smussa (per apparire in maniera più chiara), la curva dovrebbe somigliare al grafico sottostante.
4. Nell'esperimento del compleanno, poni N = 365. Per n = 10, 20, 30, 40, 50 e 60 simula 1000 replicazioni per ciascun caso, calcolando la frequenza relativa dell'evento in cui qualche cella contiene 2 o più palline. Confronta la frequenza relativa con le probabilità calcolate nell'esercizio 4.
Nonostante la sua semplice soluzione, il problema del compleanno è molto noto perché, numericamente, le probabilità possono sembrare sorprendenti. Per solo 60 persone, l'evento è quasi certo! Matematicamente, la crescita rapida delle probabilità al crescere di n, è dovuta al fatto che Nn cresce più velocemente di (N)n.
5. Si scelgono a caso 10 persone. Trova la probabilità che almeno due siano nati nella stessa settimana.
6. Nell'esperimento del compleanno, poni N = 52. Modifica n con la barra a scorrimento e osserva graficamente come le probabilità cambiano. Con n = 10, simula 1000 replicazioni, aggiornando ogni 10. Osserva la convergenza della frequenza relativa alla probabilità teorica.
7. Si lanciano quattro dadi equilibrati. Trova la probabilità che i punteggi siano distinti.
8. Nell'esperimento del compleanno, poni N = 6. Modifica n con la barra a scorrimento e osserva graficamente come le probabilità cambiano. Con n = 10, simula 1000 replicazioni, aggiornando ogni 10. Osserva la convergenza della frequenza relativa alla probabilità teorica.
9. Si scelgono a caso 5 persone. Trova la probabilità che almeno due siano nate nello stesso mese.
10. Nell'esperimento del compleanno, poni N = 12. Modifica n con la barra a scorrimento e osserva graficamente come le probabilità cambiano. Con n = 10, simula 1000 replicazioni, aggiornando ogni 10. Osserva la convergenza della frequenza relativa alla probabilità teorica.
11. Un fast-food distribuisce 10 pupazzi diversi insieme ai menu per bambini. Una famiglia con cinque bambini compra 5 menu. Trova la probabilità che i pupazzi siano tutti diversi.
12. Nell'esperimento del compleanno, poni N = 5. Modifica n con la barra a scorrimento e osserva graficamente come le probabilità cambiano. Con n = 5, simula 1000 replicazioni, aggiornando ogni 10. Osserva la convergenza della frequenza relativa alla probabilità teorica.
13. Sia bN,n la probabilità dell'evento complementare che le variabili campionarie siano distinte. Prova le seguente relazione ricorsiva in due modi: in primo luogo partendo dal risultato dell'esercizio 1, e poi utilizzando la probabilità condizionata.
14. Sia N = 52 (corrispondenti alle settimane di nascita). Trova il valore più piccolo di n per cui la probabilità di duplicazione è almeno 1/2.
15. Esegui l'esperimento del compleanno 1000 volte, con N = 52 e col valore di n ricavato nell'esercizio 14. Confronta la frequenza relativa della duplicazione col valore di probabilità.