1. Mostra che X(i)
assume valori i, i + 1, ..., N - n + i. Laboratorio virtuale > Modelli di campionamento finito > 1 2 3 4 [5] 6 7 8 9 10
Supponiamo che le unità della popolazione siano numerate da 1 a N, dimodoché D = {1, 2, ..., N}. Per esempio, la popolazione può essere formata da manufatti, e la numerazione può corrispondere ai numeri di serie. Campioniamo n unità a caso e senza reinserimento da D:
X = (X1, X2, ..., Xn), dove Xi appartenente a D è l'i-esima unità estratta.
Ricordiamo che X è distribuita uniformemente sull'insieme delle permutazioni di dimensione n estratte da D. Ricordiamo inoltre che W = {X1, X2, ..., Xn} è il campione non ordinato, distribuito uniformemente sull'insieme delle combinazioni di dimensione n estratto da D.
Per i = 1, 2, ..., n, sia X(i) l'i-esima unità minore di X1, X2, ..., Xn. La variabile casuale X(i) è detta i-esima statistica d'ordine del campione. Notiamo in particolare che X(1) è il minimo valore e X(n) il massimo.
1. Mostra che X(i)
assume valori i, i + 1, ..., N - n + i.
Indicheremo il vettore di statistiche d'ordine con
U = (X(1), X(2), ..., X(n)).
Notiamo che U assume valori in L = {(x1,
x2, ..., xn): 1 
x1 < x2 < ··· < xn
N}
2. Esegui l'esperimento delle statistiche d'ordine. Nota che puoi modificare l'ampiezza della popolazione N e l'ampiezza del campione n. Le statistiche d'ordine sono registrate ad ogni aggiornamento.
3. Mostra che L ha C(N, n) elementi e che U è distribuita uniformemente su L.
Suggerimento: U = (x1, x2,
..., xn) se e solo se W = {x1,
x2, ..., xn} se e solo se X
è una delle n! permutazioni di (x1, x2,
..., xn).
4. Usa una prova di calcolo combinatorio per mostrare che la funzione di densità di X(i) è:
P(X(i) = k) = C(k - 1, i - 1)C(N - k, n - i) / C(N, n) per k = i, i + 1, ..., N - n + i.
5. Nell'esperimento delle statistiche d'ordine, modifica i parametri e osserva la forma della funzione di densità. Con N = 30, n = 10 e i = 5, simula 1000 replicazioni, aggiornando ogni 10. Osserva la convergenza delle densità empiriche alla funzione di densità teorica.
La funzione di densità dell'esercizio 4 può essere utilizzata per ricavare un'interessante identità che riguarda i coefficienti binomiali. Tale identità può essere utilizzata per trovare media e varianza di X(i) .
5.
Mostra che per ogni i = 1, 2,
..., N,
k
= i, ..., N - n + i C(k, i)
C(N - k, n - i) = C(N + 1, n
+ 1).
6. Usa l'identità dell'esercizio 5 per mostrare che
E(X(i)) = i (N + 1) / (n + 1).
7. Usa l'identità dell'esercizio 5 per mostrare che
var(X(i)) = (N + 1)(N - n)i(n + 1 - i) / [(n + 1)2(n + 2)].
8. Nell'esperimento delle statistiche d'ordine, modifica i parametri e osserva la dimensione e la posizione della barra media/deviazione standard. Con N = 30, n = 10 e i = 5, simula 1000 replicazioni, aggiornando ogni 10. Osserva la convergenza dei momenti empirici ai loro valori teorici.
10. Supponi che, in una lotteria, si mettano biglietti numerati da 1 a 25 in un'urna. Si estraggono a caso e senza reinserimento cinque biglietti. Calcola
11. Usa il risultato dell'esercizio 6 per mostra che, per i = 1, 2, ..., n, la statistica seguente è uno stimatore corretto per N:
Wi = [(n + 1) X(i) / i] - 1.
Poiché Wi è corretto, la sua varianza è l'errore quadratico medio, una misura della qualità dello stimatore.
12. Prova che var(Wi)
= (N + 1)(N - n)(n + 1 - i) / [i(n
+ 2)]
13. Mostra che, per dati N e n, var(Wi) decresce al crescere di i.
Pertanto gli stimatori migliorano al crescere di i; in particolare, Wn è il migliore e W1 il peggiore.
14. Mostra che var(Wj)
/ var(Wi) = j(n + 1 - i) / [i(n
+ 1 - j)]
Tale rapporto è detto efficienza relativa di Wi rispetto a Wj.
Di solito si spera che gli stimatori migliorino (secondo il criterio dell'errore quadratico medio) al crescere della dimensione campionaria n (più informazioni si hanno, migliore ci si aspetta che sia la stima). Tale proprietà è detta consistenza.
15. Mostra che
var(Wn) tende a 0 per n che tende a N.
16. Mostra che, per dato i, var(Wi) prima cresce e poi decresce a 0 all'aumentare di n da 1 a N.
Il grafico seguente, dovuto a Christine Nickel, mostra var(W1) in funzione di n per N = 50, 75 e 100.
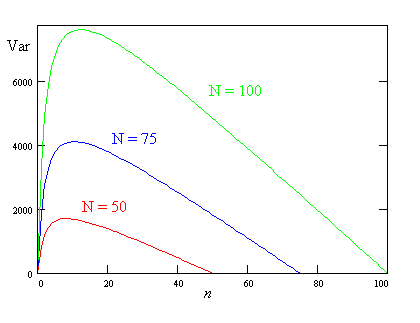
Lo stimatore Wn venne usato dagli alleati durante la seconda guerra mondiale per stimare il numero N di carri armati tedeschi prodotti. I carri armati avevano un numero di serie, e i carri catturati e i loro numeri seriali formavano i dati campionari. Seguendo Richard Larsen e Morris Marx, tale stima della produzione di carri nel 1942 fu 3400, molto vicina al numero reale.
17. Supponi che, in una guerra, vengano catturati 100 carri nemici. Il numero seriale più elevato è 1423. Stima il numero totale di carri prodotti.
18. Nell'esperimento delle statistiche d'ordine, poni N = 100 e n = 10. Simula 50 replicazioni, aggiornando ogni volta. Per ciascuna replicazione, calcola la stima di N basandoti su ciascuna delle statistiche d'ordine. Per ciascuno stimatore, calcola la radice quadrata della media dei quadrati degli errori per le 50 replicazioni. Basandoti su tali stime empiriche dell'errore, disponi gli stimatori di N in ordine di qualità.
19. Supponi che, in una guerra, vengano catturati 100 carri nemici. Il numero seriale più basso è 23. Stima il numero totale di carri prodotti.
Se il campionamento è con reinserimento, le variabili del campione X1, X2, ..., Xn sono indipendenti e identicamente distribuite. Le statistiche d'ordine da campioni di tale tipo sono studiate nel capitolo sui campioni casuali.