1. Replica l'esperimento di Bertrand 100 volte, aggiornando ogni volta, per ciascuno dei seguenti modelli. Non preoccuparti del loro significato esatto, ma cerca di trovare delle differenze di comportamento nei risultati
Laboratorio virtuale > Modelli geometrici > 1 2 [3] 4 5
Il paradosso di Bertrand consiste nel trovare la probabilità che una "corda aleatoria" di una circonferenza sia più lunga della lunghezza di uno dei lati del triangolo equilatero inscritto. Il problema prende il nome dal matematico francese Joseph Louis Bertrand, che analizzò il problema nel 1889.
Come vedremo, risultano esserci (almeno) due soluzioni al problema, ed esse dipendono dall'interpretazione che si dà alla nozione di "corda aleatoria". La mancanza di una risposta univoca era al tempo considerata un paradosso, perché si pensava (ingenuamente, a ben vedere), che dovesse esserci un'unica risposta naturale.
1. Replica l'esperimento di Bertrand 100 volte, aggiornando ogni volta, per ciascuno dei seguenti modelli. Non preoccuparti del loro significato esatto, ma cerca di trovare delle differenze di comportamento nei risultati
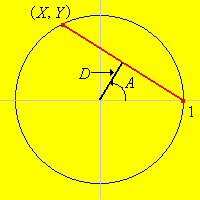
Per formulare il problema in termini matematici, assumiamo (0, 0) come centro della circonferenza e assumiamo raggio unitario. Queste assunzioni non comportano perdita di generalità, poiché introducono un sistema di misurazione relativo al centro della circonferenza e col raggio della stessa come unità di misura. Consideriamo ora una corda sulla circonferenza. Ruotando quest'ultima, possiamo assumere che uno dei punti della corda sia (1,0) e l'altro (X, Y) dove Y > 0. Possiamo allora specificare completamente la corda tramite uno delle seguenti quantità:
Nota che 0 
D 1, 0 A 
/ 2, -1 X 1.
2. Prova che D
= cos(A).
3. Mostra che X
= 2D2 - 1.
4. Mostra che Y = 2D (1 - D2)1/2.
5. Dimostra che le relazioni degli esercizi 2 e 3 sono invertibili e trova le relazioni inverse.
Se la corda è generata in maniera aleatoria, D, A, X, e Y risultano essere variabili casuali. Alla luce dell'esercizio 5, specificare la distribuzione di una qualunque delle variabili D, A o X determina completamente la distribuzione di tutte e quattro le variabili.
6. Mostra che A
è anche l'angolo formato dalla corda e la retta tangente al cerchio in (1, 0).
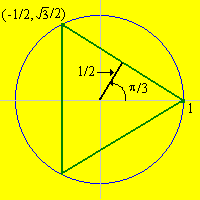
Consideriamo ora il triangolo equilatero inscritto nella circonferenza in modo che uno dei vertici sia (1, 0). Considera la corda definita dal lato superiore del triangolo.
7. Prova che, per tale corda, angolo, distanza e coordinate sono date da:
/ 3
Supponiamo ora di scegliere una corda in maniera probabilistica.
8. Utilizzando l'esercizio 7, mostra che la lunghezza della corda è maggiore della lunghezza del lato del triangolo equilatero inscritto se e solo se si verificano le seguenti condizioni:
/ 3 < A <
/ 2Quando un oggetto è generato "a caso" alla sequenza di variabili "naturali" che determina l'oggetto deve essere assegnata un'appropriata distribuzione. Le coordinate del centro della moneta sono una sequenza di questo tipo nel contesto dell'esperimento della moneta di Buffon; le variabili distanza e angolo sono una sequenza di questo tipo nell'esperimento dell'ago di Buffon. Il fatto cruciale nel paradosso di Bertrand è che la distanza D e l'angolo A sembrano essere entrambe variabili naturali per individuare la corda, ma si ottengono modelli diversi a seconda della variabile alla quale si assegna distribuzione uniforme.
Supponi che D sia distribuita uniformemente sull'intervallo (0, 1).
9. Prova che la soluzione del paradosso di Bertrand è
P(D < 1/2) = 1/2
10. Nell'
esperimento di Bertrand, seleziona il modello a distanza uniforme. Simula 1000 replicazioni, aggiornando ogni 10. Osserva la convergenza della funzione di frequenza relativa sulla corda alla probabilità vera.
11. Usa la
formula del cambiamento di variabile per mostrare che l'angolo A ha funzione di densità
g(a) = sin(a), 0 < a <
/2
12. Usa la formula del cambiamento di variabile per mostrare che X ha funzione di densità
h(x) = (1/4) [(x + 1) / 2]-1/2, -1 < x < 1.
Nota che A e X non sono distribuite uniformemente.
Supponi che A sia distribuita uniformemente sull'intervallo (0, /2).
13. Prova che la soluzione del problema di Bertrand è
P(A > / 3) = 1/3
14. Nell'esperimento di Bertrand, seleziona il modello con angolo uniforme. Simula 1000 replicazioni, aggiornando ogni 10. Osserva la convergenza della funzione di frequenza relativa sulla corda alla probabilità vera.
15. Usa la formula del cambiamento di variabile per mostrare che la distanza D ha funzione di densità
f(d) = 2 / [(1 - d2)1/2],
0 < d < 1.
16. Usa la formula del cambiamento di variabile per mostrare che X ha funzione di densità
h(x) = 1 / [(1 - x2)1/2],
-1 < x < 1.
Nota che D e X non sono uniformemente distribuite.
17. Supponi di generare una corda casuale lanciando una moneta di raggio 1 su un tavolo rigato con linee parallele a distanza 2 l'una dall'altra. Quale dei modelli (o nessuno?) si può applicare a questo esperimento?
18. Supponi di attaccare un ago al bordo di un disco di raggio 1. Si genera una corda aleatoria facendo girare l'ago. Quale dei modelli (o nessuno?) si può applicare a questo esperimento?
19. Supponi di costruire un canalino sul bordo di un disco di raggio 1. Gettare una pallina nel canale genera un punto casuale sulla circonferenza, per cui una corda aletoria si può generare lanciando due volte la pallina. Quale dei modelli (o nessuno?) si può applicare a questo esperimento?