Laboratorio virtuale > Modelli geometrici > 1 [2] 3 4 5
L'esperimento dell'ago di Buffon è un esperimento casuale antico e ben noto, che prende nome dal Compte De Buffon. L'esperimento consiste nel far cadere un ago su un pavimento di assi di legno. L'evento di interesse è che l'ago vada a cadere su un'intercapedine tra un'asse e l'altra. Stranamente, la probabilità di questo evento conduce a una stima statistica del numero pi greco!
Il primo passo consiste nel definire l'esperimento in termini matematici. Di nuovo, astraiamo gli oggetti fisici assumendo che le assi del pavimento siano identiche e di larghezza unitaria. Assumeremo inoltre che l'ago abbia lunghezza L < 1 cosicché non possa incorciare più di una fessura. Assumeremo infine che le intercapedini tra le assi siano segmenti di retta.
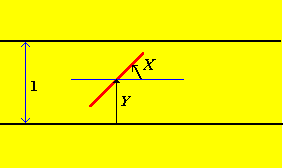
Lanciando l'ago, vogliamo registrare il suo orientamento rispetto alle fessure. Un modo per farlo è registrare l'angolo X che l'estremita superiore dell'ago forma con la retta che passa per il centro dell'ago parallela alle assi, e la distanza Y dal centro dell'ago all'intercapedine inferiore. Si tratta di variabili casuali semplice per l'esperimento, per cui lo spazio campionario è
S = (0, ![]() ) × (0, 1) = {(x,
y): 0 < x <
) × (0, 1) = {(x,
y): 0 < x < ![]() , 0 < y
< 1}
, 0 < y
< 1}
Di nuovo, l'assunzione che facciamo è di lanciare l'ago "a caso" sul pavimento. Quindi, un'assunzione matematica ragionevole può essere che il vettore aleatorio (X, Y) sia distribuito uniformemente sullo spazio campionario. Per definizione, ciò significa che
P[(X, Y) ![]() A]
= area(A) / area(S) per A
A]
= area(A) / area(S) per A ![]() S.
S.
![]() 1. Esegui l'
esperimento dell'ago di Buffon con le impostazioni predefinite e osserva gli esiti sullo spazio campionario. Osserva come i punti della dispersione sembrano riempire lo spazio campionario S
in maniera uniforme.
1. Esegui l'
esperimento dell'ago di Buffon con le impostazioni predefinite e osserva gli esiti sullo spazio campionario. Osserva come i punti della dispersione sembrano riempire lo spazio campionario S
in maniera uniforme.
L'evento di interesse C è quello in cui l'ago cade su una fessura tra le assi.
![]() 2. Usa la trigonometria per mostrare che C può essere scritto come segue in termini delle variabili angolo e distanza:
2. Usa la trigonometria per mostrare che C può essere scritto come segue in termini delle variabili angolo e distanza:
C = {Y < (L / 2)sin(X)} ![]() {Y > 1 - (L / 2)sin(X)}
{Y > 1 - (L / 2)sin(X)}
![]() 3. Usa l'analisi per mostrare che area(C) = 2L e quindi
3. Usa l'analisi per mostrare che area(C) = 2L e quindi
P(C) = 2L / ![]()
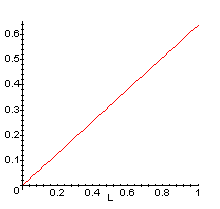
![]() 4. Usa quello che sai sulle rette per mostrare che P(C) in funzione di L,
ha il grafico seguente:
4. Usa quello che sai sulle rette per mostrare che P(C) in funzione di L,
ha il grafico seguente:
![]() 5. Trova la probabilità che l'ago non cada su una fessura.
5. Trova la probabilità che l'ago non cada su una fessura.
Le curve
y = (L / 2)sin(x), y = 1 - (L / 2)sin(x)
sono disegnate in blu nel grafico a dispersione, per cui l'evento C è l'unione delle regioni tra la curva inferiore e la curva superiore. Pertanto, l'ago cade su una fessura esattamente quando un punto cade nella regione.
![]() 6. Nell'
Buffon, modifica la lunghezza dell'ago L con la barra a scorrimento e osserva come gli eventi C e Cc cambiano. Esegui l'esperimento con diversi valori di L e confronta l'esperimento fisico coi punti della dispersione. Osserva la convergenza della frequenza relativa di C
alla probabilità di C.
6. Nell'
Buffon, modifica la lunghezza dell'ago L con la barra a scorrimento e osserva come gli eventi C e Cc cambiano. Esegui l'esperimento con diversi valori di L e confronta l'esperimento fisico coi punti della dispersione. Osserva la convergenza della frequenza relativa di C
alla probabilità di C.
La convergenza della frequenza relativa di un evento (al ripetersi dell'esperimento) alla probabilità dell'evento è un caso particolare della legge dei grandi numeri.
![]() 7. Trova le probabilità dei seguenti eventi nell'esperimento dell'ago di Buffon. In ciascun caso, disegna l'eveno come sottinsieme dello spazio campionario.
7. Trova le probabilità dei seguenti eventi nell'esperimento dell'ago di Buffon. In ciascun caso, disegna l'eveno come sottinsieme dello spazio campionario.
Supponiamo di eseguire l'esperimento dell'ago di Buffon un numero molto elevato di volte. Per la legge dei grandi numeri, la proporzione degli incroci dev'essere prossima alla probabilità di incrociare una fessura. Più precisamente, indicheremo il numero di incroci nelle prime n prove con Nn. Nota che Nn è una variabile casuale per l'esperimento composito formato da n replicazioni dell'esperiemnto semplice. Quindi, se n è grande, dovremmo avere
Nn / n ~ 2L / ![]() e quindi
e quindi ![]() ~ 2Ln / Nn.
~ 2Ln / Nn.
Questa è la celebre stima di Buffon di π. Nella simulazione, tale stima è calcolata ad ogni ciclo ed è mostrata numericamente nella seconda tabella e visualmente nel grafico a barre.
![]() 8. Esegui l'
esperimento dell'ago di Buffon con lunghezza dell'ago L = 0.3, 0.5,
0.7, e 1. In ciascun caso, osserva la stima di pi all'evolversi della simulazione.
8. Esegui l'
esperimento dell'ago di Buffon con lunghezza dell'ago L = 0.3, 0.5,
0.7, e 1. In ciascun caso, osserva la stima di pi all'evolversi della simulazione.
Analizziamo più attentamente il problema della stima. Per ciascuna esecuzione j si ha la variabile indicatore
Ij = 1 se l'ago incrocia una fessura alla j-esima replicazione; Ij = 0 altrimenti
Queste variabili indicatrici sono indipendenti e identicamente distribuite, poiché stiamo assumendo replicazioni indipendenti dell'esperimento. Quindi, la sequenza forma un processo di prove Bernoulliane.
![]() 9. Prova che il numero di incorci nelle prime n replicazioni dell'esperimento è
9. Prova che il numero di incorci nelle prime n replicazioni dell'esperimento è
Nn = I1 + I2 + ··· + In.
![]() 10. Usa il risultato dell'esercizio 9 per mostrare che il numero di incroci nelle prime n replicazioni ha distribuzione binomiale con parametri n e
10. Usa il risultato dell'esercizio 9 per mostrare che il numero di incroci nelle prime n replicazioni ha distribuzione binomiale con parametri n e
p = 2L / ![]()
![]() 11. Usa il risultato dell'esercizio 9 per mostrare che media e varianza del numero di incroci sono
11. Usa il risultato dell'esercizio 9 per mostrare che media e varianza del numero di incroci sono
![]() 12. Usa la legge forte dei grandi numeri per mostrare che
12. Usa la legge forte dei grandi numeri per mostrare che
Si hanno quindi due stimatori:
Lo stimatore (1) gode di molte importanti proprietà statistiche. In primo luogo, è corretto, poiché il valore atteso dello stimatore è pari al parametro:
![]() 13. Usa l'esercizio 11 e le proprietà del valore atteso per mostrare che
13. Usa l'esercizio 11 e le proprietà del valore atteso per mostrare che
E(Nn / 2Ln) = 1 / ![]() .
.
Poiché lo stimatore è corretto, la varianza coincide con l'errore quadratico medio:
var(Nn / 2Ln) = E[(Nn / 2Ln
- 1 / ![]() )2]
)2]
![]() 14. Usa l'esercizio 4
e le proprietà della varianza per mostrare che
14. Usa l'esercizio 4
e le proprietà della varianza per mostrare che
var(Nn / 2Ln) = (![]() - 2L) / (2L
n
- 2L) / (2L
n ![]() 2)
2)
![]() 15. Mostra che la varianza dell'esercizio 11 è funzione decrescente della lunghezza dell'ago L.
15. Mostra che la varianza dell'esercizio 11 è funzione decrescente della lunghezza dell'ago L.
L'esercizio 15 mostra che lo stimatore (1) migliora all'aumentare della lunghezza dell'ago. Lo stimatore (2) è distorto e tende a sovrastimare pi:
![]() 16. Usa la
disuguaglianza di
Jensen per provare che
16. Usa la
disuguaglianza di
Jensen per provare che
E(2Ln / Nn) ![]()
![]() .
.
Anche lo stimatore (2) migliora all'aumentare della lunghezza dell'ago, ma non è facile dimostrarlo formalmente. In ogni caso, puoi vederlo empiricamente.
![]() 17. Nell'esperimento dell'ago di Buffon, poni la frequenza di aggiornamento a 100. Simula 5000 replicazioni, con L = 0.3, L = 0.5, L = 0.7, e L
= 1. Osserva come sembra funzionare lo stimatore in ciascun caso.
17. Nell'esperimento dell'ago di Buffon, poni la frequenza di aggiornamento a 100. Simula 5000 replicazioni, con L = 0.3, L = 0.5, L = 0.7, e L
= 1. Osserva come sembra funzionare lo stimatore in ciascun caso.
Infine, dobbiamo notare che, all'atto pratico, l'esperimento dell'ago di Buffon non è un modo molto efficiente di approssimare pi. Seguendo Richard Durrett, la stima di pi con un'approssimazione di quattro posizioni decimali con L = 1 / 2 richiederebbe circa 100 milioni di lanci!
![]() 18. Simula l'esperimento dell'ago di Buffon con frequenza di aggiornamento 100 fino a che la stima di pi sembra consistentemente corretta alla seconda posizione decimale. Nota il numero di replicazioni necessarie. Prova con le lunghezze L = 0.3, L = 0.5, L = 0.7, e L = 1 e confronta i risultati.
18. Simula l'esperimento dell'ago di Buffon con frequenza di aggiornamento 100 fino a che la stima di pi sembra consistentemente corretta alla seconda posizione decimale. Nota il numero di replicazioni necessarie. Prova con le lunghezze L = 0.3, L = 0.5, L = 0.7, e L = 1 e confronta i risultati.