Laboratorio virtuale > Modelli geometrici > [1] 2 3 4 5
L'esperimento della moneta di Buffon è un esperimento casuale, molto antico e conosciuto, che prende nome dal conte di Buffon. L'esperimento consiste nel lanciare a caso una moneta su un pavimento coperto da mattonelle di identica forma. L'evento di interesse è che la moneta cada su una intercapedine tra le mattonelle. Inizieremo a modellare il problema della moneta di Buffon con il caso di mattonelle quadrate di lato 1 (assumere lunghezza del lato unitaria equivale a misurare la distanza in unità di lato).
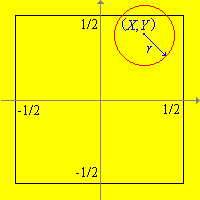
Iniziamo definendo l'esperimento in termini più formali. Come al solito, procederemo idealizzando gli oggetti fisici: assumiamo che la moneta sia un cerchio perfetto di raggio r e che le intercapedini siano segmenti di linee. Un modo naturale per descrivere l'esito dell'esperimento è registrare il centro della moneta relativamente al centro della mattonella su cui è caduta. Più precisamente, costruiremo assi di coordinate tali che la mattonella dove cade la moneta occupi il quadrato
S = [-1/2, 1/2]2 = {(x, y): -1/2 ![]() x
x ![]() 1/2, -1/2
1/2, -1/2 ![]() y
y ![]() 1/2}
1/2}
Ora, quando la moneta viene lanciata, indichiamo il suo centro con (X, Y)
![]() S cosicché S è lo
spazio campionario e X e Y sono le nostre variabili casuali. Assumiamo infine che r
< 1/2 per cui è almeno possibile che la moneta cada dentro una mattonella senza toccare una delle intercapedini.
S cosicché S è lo
spazio campionario e X e Y sono le nostre variabili casuali. Assumiamo infine che r
< 1/2 per cui è almeno possibile che la moneta cada dentro una mattonella senza toccare una delle intercapedini.
Ora dobbiamo definira una misura di probabilità appropriata per il nostro vettore aleatorio (X, Y). Se la moneta è gettata "a caso" sul pavimento, è naturale assumere che (X, Y) sia distribuita uniformemente su S. Per definizione ciò significa che
P[(X, Y) ![]() A]
= area(A) / area(S) per A
A]
= area(A) / area(S) per A ![]() S.
S.
![]() 1. Esegui l'esperimento della moneta di Buffon con le impostazioni predefinite. Osserva come i punti finiscono per riempire lo spazio campionario S in maniera uniforme.
1. Esegui l'esperimento della moneta di Buffon con le impostazioni predefinite. Osserva come i punti finiscono per riempire lo spazio campionario S in maniera uniforme.
Il nostro interesse è puntato sull'evento C in cui la moneta cade su un intercapedine. In ogni caso, sembra più semplice descrivere l'evento complementare, in cui la moneta non incrocia nessuna fessura.
![]() 2. Mostra che
2. Mostra che
Cc = {r - 1/2 < X < 1/2 - r, r - 1/2 < Y < 1/2 - r}
![]() 3. Usa il risultato dell'esercizio 2 per mostrare che
3. Usa il risultato dell'esercizio 2 per mostrare che
![]() 4. Usa l'analisi
(o ciò che sai sulle parabole) per provare che P(C), in funzione di r,
ha il grafico sotto riportato:
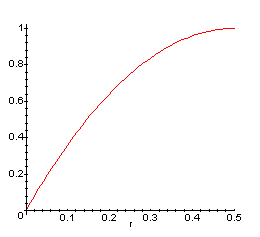
4. Usa l'analisi
(o ciò che sai sulle parabole) per provare che P(C), in funzione di r,
ha il grafico sotto riportato:
![]() 5. Nell'esperimento della moneta di Buffon, modifica il raggio con la barra a scorrimento e osserva come variano gli eventi C e Cc. Simula l'esperimento con diversi valori di r e confronta l'esperimento fisico coi punti della dispersione. Osserva la convergenza della frequenza relativa di C alla probabilità di C.
5. Nell'esperimento della moneta di Buffon, modifica il raggio con la barra a scorrimento e osserva come variano gli eventi C e Cc. Simula l'esperimento con diversi valori di r e confronta l'esperimento fisico coi punti della dispersione. Osserva la convergenza della frequenza relativa di C alla probabilità di C.
La convergenza della frequenza relativa di un evento (al ripetersi dell'esperimento) alla probabilità dell'evento è un caso particolare della legge dei grandi numeri.
![]() 6. Risolvi il problema della moneta di Buffon nel caso di mattonelle rettangolari di altezza h e base w.
6. Risolvi il problema della moneta di Buffon nel caso di mattonelle rettangolari di altezza h e base w.
![]() 7. Risolvi il problema della moneta di Buffon nel caso di mattonelle triangolari di lato 1.
7. Risolvi il problema della moneta di Buffon nel caso di mattonelle triangolari di lato 1.