Laboratorio virtuale > Modelli geometrici > 1 2 3 [4] 5
Supponiamo di spezzare un bastoncino in due punti: qual è la probabilità che i tre pezzi formino un triangolo?
![]() 1.
Prova a indovinare senza guardare più avanti.
1.
Prova a indovinare senza guardare più avanti.
![]() 2. Replica l'esperimento del triangolo 50 volte. Non preoccuparti delle altre informazioni riportate nell'applet, nota solamente quando i pezzi formano un triangolo. Vuoi rivedere la tua risposta all'esercizio 1?
2. Replica l'esperimento del triangolo 50 volte. Non preoccuparti delle altre informazioni riportate nell'applet, nota solamente quando i pezzi formano un triangolo. Vuoi rivedere la tua risposta all'esercizio 1?
Al solito, il primo passo è di formalizzare l'esperimento casuale. Consideriamo la lunghezza del bastoncino come unità di misura, in modo da poter identificare il bastoncino con l'intervallo [0, 1]. Per rompere il bastoncino in tre pezzi basta scegliere due punti. Sia quindi X il primo punto e Y il secondo. Notiamo che X e Y sono variabili casuali e quindi lo spazio campionario del nostro esperimento è
S = [0, 1]2.
Ora, per rappresentare il fatto che i punti sono selezionati a caso, assumiamo, come nei paragrafi precedenti, che X e Y siano indipendenti e distribuite uniformemente su [0, 1].
![]() 3. Prova che (X, Y)
è distribuito uniformemente su S = [0, 1]2.
3. Prova che (X, Y)
è distribuito uniformemente su S = [0, 1]2.
Quindi, P(A)
= area(A) / area(S) = area (A) per A ![]() S.
S.
![]() 4. Spiega perché i tre pezzi formano un triangolo se e solo se valgono le disuguaglianze triangolari: la somma delle lunghezze di due qualunque dei pezzi dev'essere maggiore della lunghezza del terzo.
4. Spiega perché i tre pezzi formano un triangolo se e solo se valgono le disuguaglianze triangolari: la somma delle lunghezze di due qualunque dei pezzi dev'essere maggiore della lunghezza del terzo.
![]() 5. Prova che l'evento in cui i tre pezzi formano un triangolo è T = T1
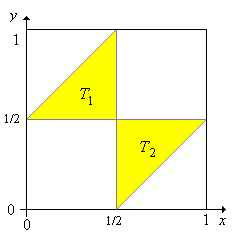
5. Prova che l'evento in cui i tre pezzi formano un triangolo è T = T1 ![]() T2 dove
T2 dove
Un grafico dell'evento T è riportato qui sotto:
![]() 6. Prova che P(T)
= 1/4.
6. Prova che P(T)
= 1/4.
Quanto ti sei avvicinato nell'esercizio 1? Il valore di probabilità relativamente basso dell'esercizio 6 è abbastanza sorprendente.
![]() 7. Replica l'esperimento del triangolo 1000 volte, aggiornando ogni 10 replicazioni. Osserva la convergenza della probabilità empirica di Tc al valore teorico.
7. Replica l'esperimento del triangolo 1000 volte, aggiornando ogni 10 replicazioni. Osserva la convergenza della probabilità empirica di Tc al valore teorico.
Calcoliamo ora la probabilità che i pezzi formino un triangolo di un dato tipo. Ricorda che in un triangolo acutangolo tutti e tre gli angoli misurano meno di 90°, mentre un triangolo ottusangolo ha uno e un solo angolo maggiore di 90°. Un triangolo rettangolo, ovviamente, ha un angolo di 90°.
![]() 8.
Supponi che un triangolo abbia lati di lunghezza a, b e c, dove
c è il valore maggiore. Ricorda (o prova) che il triangolo è
8.
Supponi che un triangolo abbia lati di lunghezza a, b e c, dove
c è il valore maggiore. Ricorda (o prova) che il triangolo è
La parte (c), ovviamente, è il celebre teorema di Pitagora, che prende nome dal celebre matematico greco Pitagora.
![]() 9. Prova che le equazioni del triangolo rettangolo per i pezzi sono
9. Prova che le equazioni del triangolo rettangolo per i pezzi sono
![]() 10. Sia R
l'evento in cui i pezzi formano un triangolo rettangolo. Prova che
10. Sia R
l'evento in cui i pezzi formano un triangolo rettangolo. Prova che
P(R) = 0.
![]() 11. Prova che l'evento in cui i pezzi formano un triangolo acutangolo è A = A1
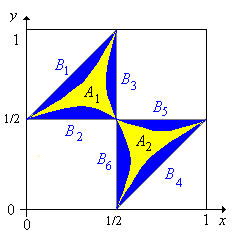
11. Prova che l'evento in cui i pezzi formano un triangolo acutangolo è A = A1 ![]() A2 dove
A2 dove
![]() 12. Prova che l'evento in cui i pezzi formano un triangolo ottusangolo è B = B1
12. Prova che l'evento in cui i pezzi formano un triangolo ottusangolo è B = B1
![]() B2
B2 ![]() B3
B3 ![]() B4
B4
![]() B5
B5 ![]() B6 dove
B6 dove
![]() 13. Prova che
13. Prova che
![]() 14. Spiega con la simmetria che
14. Spiega con la simmetria che
P(B) = 9 / 4 - 3 ln(2) ~ 0.1706
Puoi anche spiegare perché P(Bi) dev'essere lo stesso per ogni i, anche se B1 e B2 (per esempio) non sono congruenti.
![]() 15.
Prova che
15.
Prova che
P(A) = 3 ln(2) - 2 ~ 0.07944.
![]() 16. Replica l'esperimento del triangolo 1000 volte, aggiornando ogni 10. Osserva a convergenza delle probabilità empiriche ai loro valori teorici.
16. Replica l'esperimento del triangolo 1000 volte, aggiornando ogni 10. Osserva a convergenza delle probabilità empiriche ai loro valori teorici.