Laboratorio virtuale > Spazi di Probabilità > 1 2 3 4 [5] 6 7 8
Al solito, iniziamo introducendo un esperimento casuale
con spazio campionario S, e misura di probabilità P. Supponiamo inoltre di sapere che un certo evento B si è verificato. In genere, questa informazione dovrebbe alterare le probabilità che assegniamo agli altri eventi. In particolare, se A è un altro evento, allora A si verifica se e solo se si verificano sia A che B;
di fatto, lo spazio campionario si è ridotto a B. Quindi, la probabilità di A, data la conoscenza del fatto che B si è verificato, dovrebbe essere proporzionale a P(A 
B).
In ogni caso, la probabilità condizionata, dato il verificarsi di B dev'essere sempre una misura di probabilità, ovvero deve soddisfare gli assiomi di Kolmogorov. Ciò fa sì che la costante di proporzionalità debba essere 1 / P(B). Pertanto, si giunge inesorabilmente alla seguente definizione:
Siano A ae B eventi di un esperimento casuale con P(B) > 0. La probabilità condizionata di A dato B è definita come
P(A | B) = P(A B) / P(B).
Ciò si basa sulla definizione assiomatica di probabilità. Analizziamo ora il concetto di probabilità condizionata a partire dalla nozione meno formale e più intuitiva di frequenza relativa. Supponiamo quindi di replicare ripetutamente l'esperimento. Per un certo evento C, sia Nn(C) il numero di volte che C si verifica nelle prime n prove.
Se Nn(B) è grande, la probabilità condizionata che A si sia verificato dato il verificarsi di B dev'essere prossima alla frequenza relativa condizionata di A dato B, ovvero la frequenza relativa di A per le prove in cui B si è verificato:
Nn(A B)
/ Nn(B).
Ma per un'altra applicazione del concetto di frequenza relativa,
P(A 
.
che ci porta di nuovo alla medesima definizione.
In alcuni casi, le probabilità condizionate possono essere calcolate direttamente, riducendo effettivamente lo spazio campionario all'evento dato. In altri casi, la formula sopra è migliore.
1. Dimostra che P(A | B), in funzione di A e per B dato, è una misura di probabilità.
L'esercizio 1 costituisce la proprietà più importante della probabilità condizionata, poiché indica che ogni risultato che vale per le misure di probabilità in generale vale anche per la probabilità condizionata (almeno finché l'evento a cui si condiziona rimane fisso).
2. Supponi che A e B siano eventi di un esperimento casuale con P(B) > 0.
Dimostra che:
A allora P(A
| B) = 1. B allora P(A
| B) = P(A) / P(B). 3. Supponi che A
e B siano eventi di un esperimento casuale, ciascuno con probabilità positiva. Dimostra che
P(B | A) > P(B)
P(A
B) > P(A)P(B)
P(B | A) < P(B)
P(A
B) < P(A)P(B)
P(B | A) = P(B)
P(A
B) = P(A)P(B)Nel caso (a), A e B si dicono positivamente correlati. Intuitivamente, il verificarsi di uno dei due eventi implica che l'altro è più probabile. Nel caso (b), A e B si dicono negativamente correlati. Intuitivamente, il verificarsi di uno dei due eventi implica che l'altro è meno probabile. Nel caso (c), A e B si dicono indipendenti. Intuitivamente, il verificarsi di uno dei due eventi non modifica le probabilità dell'altro evento.
A volte le probabilità condizionate sono note e possono essere utilizzate per trovare le probabilità di altri eventi.
4. Supponi che A1,
A2, ..., An siano eventi di un esperimento casuale la cui intersezione ha probabilità positiva. Prova la regola del prodotto della probabilità.
P(A1 A2 ··· An) = P(A1)P(A2 | A1)P(A3 | A1 A2) ··· P(An | A1 A2 ··· An-1)
La regola del prodotto è molto utile negli esperimenti formati da stadi dipendenti, dove Ai è un evento dell'i-esimo stadio. Confronta la regola del prodotto della probabilità con la regola del prodotto del calcolo combinatorio.
5.
Supponi che A
e B siano eventi di un esperimento con P(A) = 1 / 3, P(B) = 1 / 4, P(A
B) = 1 / 10.
Trova:
6. Considera l'esperimento consistente nel lanciare due dadi equilibrati e registrare la sequenza di punteggi
La correlazione non è transitiva. Nota per esempio, nell'esercizio precedente, che {X1 = 3}, {Y = 5} sono positivamente correlati, {Y = 5}, {X1 = 2} sono positivamente correlati, ma {X1 = 3}, {X1 = 2} sono negativamente correlati.
7. Nell'esperimento dei dadi, poni n = 2 e simula 500 replicazioni. Calcola le probabilità condizionate empiriche corrispondenti alle condizioni dell'esercizio precedente.
8.
Considera l'esperimento delle carte che consiste nell'estrarre 2 carte da un mazzo standard e registrare la sequenza di carte estratte. Per i = 1, 2,
sia Qi l'evento in cui la carta i-esima è una regina e Hi
l'evento in cui la carta i-esima è di cuori. Per ciascuna delle seguenti coppie di eventi, calcola la probabilità di ogni evento e la probabilità condizionata di ciascun evento dato l'altro. Determina se gli eventi sono correlati postiviamente, negativamente oppure sono indipendenti.
9. Nell'esperimento delle carte, poni n = 2 e simula 500 replicazioni. Calcola le probabilità condizionate empiriche corrispondenti alle condizioni dell'esercizio precedente.
10. Considera l'esperimento delle carte con n = 3 cards. Trova la probabilità dei seguenti eventi:
11. Nell'esperimento delle carte, poni n = e simula 1000 replicazioni. Calcola la probabilità empirica di ciascun evento dell'esercizio precedente e confronta con la probabilità teorica.
12.
In un certo gruppo di persone, il 30% fuma e l'8% ha una certa malattia cardiaca. Inoltre, il 12% di coloro che fumano hanno la malattia.
13. Supponi che A, B e C siano eventi di un esperimento casuale con
B | C) = 1 / 4.
Bc
| C)
B |
C)
Bc | C). 14.
Supponi che A e B siano eventi di un esperimento casuale con P(A)
= 1 / 2, P(B) = 1 /3 , P(A | B) = 3 / 4.
Trova
B).
B).
Ac). 
15. Sui dati M&M, trova la probabilità empirica che un pacchetto contenga almeno 10 pastiglie rosse, dato un peso del pacchetto maggiore di 48 grammi.
16. Sui dati della cicala,
Supponiamo, di nuovo, di avere un esperimento con spazio campionario S e misura di probabilità P. Supponiamo che X sia una variabile casuale a valori in T relativa all'esperimento. Ricorda che la distribuzione di probabilità di X è la misura di probabilità su T data da
P(X
B) per B
T.
Analogamente, se A è un evento con probabilità positiva, la distribuzione condizionata di X dato A è la misura di probabilità su T data da
P(X
B | A)
per B
T.
17.
Considera l'esperimento consistente nel lanciare due dadi equilibrati e registrare la sequenza dei punteggi
18.
Supponi che il tempo X (in minuti) necessario per eseguire una certa operazione sia distribuito uniformemente sull'intervallo
19. Ricorda che l'esperimento della moneta di Buffon consiste nel lanciare una moneta di raggio r 
1/2 su un pavimento coperto di mattonelle quadrate di lato 1. Si registrano le coordinate (X, Y) del centro della moneta, relativamente ad assi che passano attraverso il centro del quadrato e paralleli ai lati.
20. Replica l'esperimento della moneta di Buffon 500 volte. Calcola la probabilità empirica che
Supponiamo che {Aj: j
J} sia una collezione numerabile di eventi che partiziona lo spazio campionario S.
Sia B un altro evento, e supponiamo di conoscere P(Aj) e P(B | Aj)
per ogni j J.
21.
Prova la legge delle probabilità totali:
P(B) = 
j
P(Aj)
P(B | Aj).
22.
Prova il
teorema di Bayes, che prende nome da Thomas Bayes:
per k J,
P(Ak | B) = P(Ak)P(B | Ak)
/ j
P(Aj)
P(B | Aj).
Nel contesto del teorema di Bayes, P(Aj) è la probabilità a priori di Aj e P(Aj | B) è la distribuzione a posteriori di Aj. Studieremo delle versioni più generali della legge delle probabilità totali e del teorema di Bayes nel capitolo sulle distribuzioni.
23. Nell'esperimento dado-moneta, si lancia un dado equilibrato e poi una moneta bilanciata il numero di volte indicato dal dado
24. Simula l'esperimento dado-moneta 200 volte.
25. Supponi che un sacchetto contenga 12 monete: 5 sono equilibrate, 4 sono sbilanciate con probabilità di testa 1/3 e 3 hanno due teste. Si sceglie a caso una moneta dal sacchetto e la si lancia.
Confronta gli esercizi 23 e 25. Nell'esercizio 23, si lancia una moneta con probabilità prefissata di testa un numero casuale di volte. Nell'esercizio 25, si lancia una moneta con probabilità casuale di testa un numero prefissato di volte.
26. L'esperimento moneta-dado consiste nel lanciare una moneta equilibrata; se esce croce, si lancia un dado equilibrato, se esce testa si lancia un dado piatto uno-sei (1 e 6 hanno probabilità 1/4, mentre 2, 3, 4, 5 hanno probabilità 1/8).
27. Simula l'esperimento moneta-dado
500 volte.
28. Una fabbrica ha tre linee produttive che producono chip di memoria. La prima linea produce il 50% dei chip e ha un tasso di pezzi difettosi del 4%, la seconda linea produce il 30% dei chip e ha un tasso di pezzi difettosi del 5% mentre la terza linea produce il 20% dei chip e ha un tasso di pezzi difettosi del 1%. Si estrae casualmente un chip.
29.
La forma più comune di daltonismo (dicromatismo) è una patologia ereditaria legata al sesso causata da un difetto sul cromosoma X; è quindi più comune nei maschi che nelle femmine: il 7% dei maschi sono daltonici, mentre solo lo 0.5% delle femmine lo sono. (Per ulteriori approfondimenti sulle patologie ereditarie legate al sesso, confronta la trattazione dell'emofilia.)
In un certo gruppo di persone, il 50% sono maschi e il 50% femmine.
30. Un'urna contiene inizialmente 6 palline rosse e 4 palline verdi. Si sceglie a caso una pallina e poi la si rimette nell'urna insieme ad altre due palline dello stesso colore; il processo viene poi ripetuto. Questo è un esempio di schema dell'urna di Pólya, che prende il nome da George
Pólya.
31. L'urna 1 contiene 4 palline rosse e 6 verdi, mentre l'urna 2 contiene 7 palline rosse e 3 verdi. Si sceglie a caso un urna e se ne estrae una pallina.
32. L'urna 1 contiene 4 palline rosse e 6 verdi, mentre l'urna 2 contiene 6 palline rosse e 3 verdi. Si sceglie a caso una pallina dall'urna 1 e la si insierisce nell'urna 2. Si estrae quindi una pallina dall'urna 2.
Supponiamo di avere un esperimento casuale con un evento di interesse A. Ovviamente, quando si esegue l'esperimento l'evento A può verificarsi oppure no. In ogni caso, non possiamo osservare direttamente il verificarsi o il non verificarsi di A. Disponiamo invece di un test progettato per indicare l'occorrenza dell'evento A; il test può essere o positivo per A o negativo per A. Il test ha inoltre un elemento di aleatorietà, e può dare indicazioni errate. Presentiamo alcuni esempi delle situazioni che vogliamo rappresentare:
Sia T l'evento in cui il test è positivo per il verificarsi di A. La probabilità condizionata P(T | A) è detta sensitività del test. La probabilità complementare
P(Tc | A) = 1 - P(T | A)
è la probabilità di un falso negativo. La probabilità condizionata P(Tc | Ac) è detta specificità del test. La probabilità complementare
P(T | Ac) = 1 - P(Tc | Ac)
è la probabilità di un falso positivo. In molti casi, sensitività e specificità del test sono note e sono un risultato della costruzione dello stesso. In ogni caso, l'utente del test è interessato alle probabilità condizionate opposte:
P(A | T), P(Ac|Tc).
33. Usa il teorema di Bayes per dimostrare che
P(A | T) = P(T | A)P(A) / [P(T | A)P(A) + P(T | Ac)P(Ac)].
Per fare un esempio concreto, supponiamo che la sensitività del test sia 0.99 e la specificità sia 0.95. A occhio, il test sembra buono.
34.
Trova P(A | T) in funzione di p = P(A).
Mostra che il grafico ha la seguente forma:
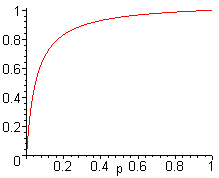
35.
Dimostra che P(A | T) in funzione di P(A)
ha i valori riportati nella seguente tabella:
| P(A) | P(A | T) |
|---|---|
| 0.001 | 0.019 |
| 0.01 | 0.167 |
| 0.1 | 0.688 |
| 0.2 | 0.832 |
| 0.3 | 0.895 |
Il valore modesto di P(A | T) per valori piccoli di P(A) cattura l'attenzione. La morale, ovviamente, è che P(A | T) dipende anche da P(A), non solo dalla sensitività e specificità del test. Inoltre, il confronto corretto è P(A | T) con P(A), come nella tabella, non P(A | T) con P(T | A).