B)
= P(A)P(B).Laboratorio virtuale > Spazi di Probabilità > 1 2 3 4 5 [6] 7 8
Al solito, iniziamo introducendo un esperimento casuale con spazio campionario S, e misura di probabilità P. In questo paragrafo, parleremo di indipendanza, uno dei concetti più importanti nella teoria della probabilità. Spesso l'indipendenza viene chiamata in causa come assunzione a priori del modello, e inoltre, come abbiamo già osservato diverse volte, l'idea stessa di probabilità fa perno su replicazioni indipendenti di un esperimento.
Due eventi A e B sono indipendenti se
P(A B)
= P(A)P(B).
Se entrambi gli eventi hanno probabilità positiva, allora affermare l'indipendenza equivale ad affermare che la probabilità condizionata di un evento dato l'altro è uguale alla probabilità non condizionata:
P(A | B) = P(A) se e solo se
P(B | A) = P(B) se e solo se P(A B) = P(A)P(B)
Puoi pensare l'indipendenza in questa maniera: sapere che un evento si è verificato non modifica la probabilità assegnata all'altro evento.
1. Considera l'esperimento consistente nell'estrarre 2 carte da un mazzo standard e registrare la sequenza di carte estratte. Per i = 1, 2,
sia Qi l'evento in cui la carta i-esima è una regina e Hi
l'evento in cui la carta i-esima è di cuori. Determina se le coppie di eventi sono indipendenti, poistivamente correlate o negativamente correlate. Interpreta i risultati.
2. Nell'esperimento delle carte, poni n = 2 e simula 500 replicazioni. Per ciascuna delle coppie di eventi dell'esercizio precedente, calcola il prodotto delle probabilità empiriche e la probabilità empirica dell'intersezione. Confronta i risultati.
I termini indipendenti e disgiunti sembrano simili, ma sono in realtà molto diversi. In primo luogo, la disgiunzione è un concetto proprio della teoria degli insiemi, mentre l'indipendenza è un concetto della teoria della probabilità (quindi basato sulla misura). All'atto pratico, due eventi possono essere indipendenti relativamente a una misura di probabilità e dipendenti rispetto a un'altra misura. E, il che è più importante, due eventi disgiunti non sono mai indipendenti, a parte un caso triviale.
3. Supponi che A e B siano eventi disgiunti in un esperimento, ciascuno con probabilità positiva. Dimostra che A e B sono negativamente correlati e quindi dipendenti.
Se A e B sono eventi indipendenti di un esperimento, sembra evidente che ogni evento che può essere costruito a partire da A debba essere indipendente da ogni evento costruito a partire da B. L'esercizio seguente dimostra questa intuizione.
4. Supponi che A e B siano eventi indipendenti dell'esperimento. Mostra che ciascuna delle seguente coppie di eventi è indipendente:
5.
Una piccola azienda ha 100 dipendenti, 40 sono uomini e 60 donne. Ci sono 6 dirigenti maschi. Quanti dirigenti femmine ci dovrebbero essere se sesso e posizione fossero indipendenti? (L'esperimento sottostante consiste nell'estrarre a caso un dipendente).
6.
Supponi che A sia un evento per cui P(A) = 0 o P(A)
= 1, e B un altro evento dell'esperimento. Dimostra che A
e B sono indipendenti.
Dall'ultimo esercizio, un evento A con P(A) = 0 o P(A) = 1 è indipendente da se stesso. Vale anche il contrario:
7.
Supponi che A sia un evento dell'esperimento e che A sia indipendente da se stesso. Mostra che o P(A) = 0 o P(A)
= 1.
8.
Considera l'esperimento che consite nel lanciare due dadi bilanciati e registrare la sequenza di punteggi. Sia A l'evento in cui il primo punteggio è 3, B l'evento in cui il secondo punteggio è 4 e C l'evento in cui la somma dei punteggi è 7.
B implica (è sottinsieme di) C.
9. Nell'esperimento dei dadi, poni n = 2 e simula 500 replicazioni.
Per ciascuna delle coppie di eventi dell'esercizio precedente, calcola il prodotto delle probabilità empiriche e la probabilità empirica dell'intersezione. Confronta i risultati.
L'esercizio 8 mostra che una collezione di eventi può essere indipendenti a due a due, ma la combinazione di due degli eventi può essere messa in relazione con un terzo evento. Dobbiamo quindi ridefinire il concetto di indipendenza per includere l'indipendenza reciproca di tre o più eventi.
Supponi che {Aj: j 
J} sia una collezione di eventi, dove J è un insieme di indici non vuoto. Gli
{Aj: j
J} si dicono indipendenti
se per ogni sottinsieme finito K di J,
P[
k
in K Ak] =
k
in K P(Ak).
10. Prova che esistono 2n - n - 1 condizioni non elementari nella definizione di indipendenza di n eventi.
11. Indica esplicitamente le 4 condizioni che devono essere soddisfatte affinché gli eventi A, B e C siano indipendenti.
12. Indica esplicitamente le 11 condizioni che devono essere soddisfatte affinché gli eventi A, B, C e D siano indipendenti.
In particolare, se A1, A2, ..., An sono indipendenti, allora
P(A1
A2
··· An)
= P(A1) P(A2) ··· P(An).
Questa è nota come regola del prodotto per eventi indipendenti. Confrontala con la regola del prodotto generale per la probabilità condizionata.
13. Supponi che A,
B e C siano eventi indipendenti di un esperimento, con P(A) =
0.3, P(B) = 0.5, P(C) = 0.8. Esprimi ciascuno dei seguenti eventi in notazione insiemistica e trova la sua probabilità:
La definizione generale di indipendenza è equivalente alla seguente condizione che implica solo l'indipendenza di coppie di eventi: se J1 e J2
sono sottinsiemi numerabili e disgiunti dell'insieme di indici J, e se B1 è un evento costruito a partire dagli eventi Aj, j J1
(utilizzando le operazioni sugli insiemi di unione, intersezione e complementazione) e B2
è un evento costruito dagli eventi Aj, j
J2, allora B1 e B2 sono indipendenti.
14. Supponi che A,
B, C e D siano eventi indipendenti di un esperimento. Prova che i seguenti eventi sono indipendenti:
A 
B, C Dc.
Il problema seguente riporta una formula per la probabilità dell'unione di eventi indipendenti molto migliore della formula di inclusione-esclusione.
15. Supponi che A1,
A2, ..., An siano eventi indipendenti. Prova che
P(A1 A2
··· An) = 1 - [1 - P(A1)][1
- P(A2)] ··· [1 - P(An)].
16. Supponi che
{Aj: j
J} sia una collezione numerabile di eventi, ciascuno dei quali con probabilità 0 o 1. Dimostra che gli eventi sono indipendenti.
17. Supponi che A,
B e C siano eventi indiependenti di un esperimento con P(A)
= 1/2, P(B) = 1/3, P(C) = 1/4. Trova la probabilità di ciascuno dei seguenti eventi:
B)
C. Bc
C.
Bc)
Cc.
18. Tre studenti dello stesso corso non si presentano a un esamino di matematica. Decidono di mentire al professore dicendo di aver bucato una gomma della macchina. Il professore separa gli studenti e chiede a ognuno quale ruota si fosse bucata. Gli studenti, che non si aspettavano tale domanda, rispondono casualmente e indipendentemente l'uno dal'altro. Trova la probabilità che gli studenti riescano a farla franca.
Per una trattazione più completa del problema degli studenti che mentono, vedi il numero di valori campionari distinti nel capitolo sui modelli di campionamento finiti.
Supponiamo, di nuovo, di avere un esperimento casuale con spazio campionario S e misura di probabilità P. Supponiamo inoltre che Xj sia una variabile casuale a valori in Tj per ogni j di un insieme non vuoto di indici J. Intuitivamente, le variabili casuali sono indipendenti se la conoscenza dei valori assunti da alcune delle variabili non ci dice nulla sul valore che le altre potranno assumere. Matematicamente, l'indipendenza di vettori aleatori può essere ricondotta all'indipendenza di eventi. Formalmente, la collezione di variabili casuali
{Xj:
j
J}
è indipendente se ogni collezione di eventi della seguente forma è indipendente:
{{Xj
Bj}: j
J} dove Bj 
Tj
for j
J.
Quindi, se K è sottinsieme finito di J allora
P[k
in K {Xk
Bk}] = k
in K P(Xk
Bk)
19. Considera una collezione di variabili casuali indipendenti definita come sopra, e supponi che per ogni j appartenente a J, gj sia una funzione da Tj in un insieme Uj. Dimostra che anche la seguente collezione di variabili casuali è indipendente.
{gj(Xj): j
J}.
20. Dimostra che la collezione di eventi {Aj, j
J} è indipendente se e solo se la collezione corrispondente di variabili indicatore
{Ij, j
J} è indipendente.
Possiamo ora precisare meglio molti dei concetti che abbiamo fin qui utilizzato informalmente. Un esperimento composto formato da "stadi indipendenti" è sempliceente un esperimento in cui la variabile esito ha forma
Y = (X1, X2, ..., Xn)
dove X1, X2, ..., Xn sono indipendenti (Xi è l'esito dell'i-esimo stadio).
In particolare, supponiamo di avere un esperimento semplice con variabile di esito X. Per definizione, l'esperimento formato da n "replicazioni indipendenti" dell'esperimento semplice ha vettore esito
Y = (X1, X2, ..., Xn)
dove Xi è distribuito come X per i = 1, 2, ..., n.
Da un punto di vista statistico, supponiamo di avere una popolazione di unità statistiche e un vettore di misurazioni di interesse sulle unità del campione. Per definizione, un "campione casuale" di dimensione n è l'esperimento il cui vettore esito è
Y = (X1, X2, ..., Xn)
dove X1, X2, ..., Xn sono indipendenti e identicamente distribuite (Xi è il vettore di misure sull'i-esima unità del campione).
Per definizione, le prove Bernoulliane sono variabili indicatore indipendenti e identicamente distribuite I1, I2, .... Più in generale le, prove multinomiali sono variabili indipendenti e identicamente distribuite X1, X2, ... che assumono valori in un insieme con k elementi (i possibili esiti della prova). In particolare, se si lanciano dadi o monete, possiamo in genere assumere che i punteggi che si ottengono siano indipendenti.
21.
Supponiamo di lanciare 5 volte un dado equilibrato. Trova la probabilità che esca almeno un 6.
22.
Supponiamo di lanciare 10 volte due dadi equilibrati. Trova la probabilità di ottenere almeno un doppio 6.
23.
Una moneta squilibrata con probabilità di testa 1/3 viene lanciata 5 volte. Sia X
il numero di teste. Trova
P(X = i) for i = 0, 1, 2, 3, 4, 5.
24. Considera l'espeirmento consistente nel lanciare n dadi e registrare la sequenza di punteggi (X1, X2, ..., Xn). Prova che le seguenti condizioni sono equivalenti (e corrispondono all'assunzione che i dadi siano equilibrati):
25.
Ricorda che l'esperimento della moneta di Buffon consiste nel lanciare una moneta di raggio r 
1/2 su un pavimento coperto da mattonelle quadrate di lato 1. Si registrano le coordinate (X, Y) del centro della moneta, relativamente ad assi che passano attraverso il centro del quadrato e paralleli ai lati. Prova che le seguenti condizioni sono equivalenti:
26. Nell'esperimento della moneta di Buffon, poni r = 0.3 e simula 500 replicazioni. Per gli eventi {X > 0}, {Y < 0}, calcola il prodotto delle probabilità empiriche e la probabilità empirica dell'intersezione. Confronta i risultati.
27. L'orario di arrivo X del treno A è distribuito uniformemente sull'intervallo (0,
30), mentre l'orario di arrivo Y del treno B è distribuito uniformemente sull'intervallo (15, 60) (gli orari di arrivo sono in minuti dopo le
8 del mattino). Inoltre, gli orari di arrivo sono indipendenti.
Gli esercizi seguenti presentano un'interssante interpretazione della probabilità condizionata. Iniziamo con un esperimento semplice, e replichiamolo indefinitamente. Quindi, se A è un evento dell'esperimento semplice, l'esperimento composto è formato da copie indipendenti di A:
A1, A2, A3, ... con P(Ai) = P(A) per ogni i.
Supponiamo ora che A e B siano eventi dell'esperimento semplice con P(B) > 0.
28.
Dimostra che, nell'esperimento composto, l'evento in cui "quando B si verifica per la prima volta, si verifica anche A" è
(A1 B1)
(B1c
A2 B2)
(B1c
B2c
A3 B3)
···
29. Dimostra che la probabilità dell'evento dell'esercizio precedente è P(A B)
/ P(B) = P(A | B).
30. Prova a spiegare direttamente il risultato dell'ultimo esercizio. In particolare, supponi di ripetere l'esperimento semplice finché B si verifica per la prima volta e poi registrare solo l'esito di questa prova. Spiega poi perché la misura di probabilità appropriata è
A 
P(A
| B).
31. Supponi che A
e B siano eventi disgiunti di un esperimento con P(A) >
0, P(B) > 0. Nell'esperimento composto che si ottiene replicando l'esperimento semplice, prova che l'evento "A si verifica prima di B"
ha probabilità
P(A) / [P(A) + P(B)].
32. Si lanciano due dadi equilibrati. Trova la probabilità che il punteggio-somma 4 si presenti prima del punteggio-somma 7.
I problemi del tipo dell'esercizio precedente sono comuni nel gioco di craps.
Come abbiamo notato all'inizio del paragrafo l'indipendenza di eventi o variabili casuali dipende dalla misura di probabilità sottostante. Supponiamo che B un evento di un esperimento casuale con probabilità positiva. Una collezione di eventi o una collezione di variabili casuali è condizionatamente indipendente dato B se la collezione è indipendente rispetto alla misura di probabilità condizionata
A P(A
| B).
Osserva che le definizioni e i teoremi di questo paragrafo restano validi, ma con tutte le probabilità condizionate a B.
33.
Una scatola contiene una moneta equilibrata e una moneta a due teste. Si estrae una moneta a caso e la si lancia ripetutamente. Sia F l'evento in cui si estrae la moneta bilanciata, e Hi l'evento in cui esce testa all'i-esimo lancio.
H2
··· Hn)
= (1 / 2)n + 1 + (1 / 2).
H2
··· Hn)
= 1 / (2n + 1).Ulteriori applicazioni dell'indipendenza condizionata sono riportate qui sotto.
In un modello semplice di affidabilità strutturale, un sistema è formato da n componenti, ciascuno dei quali, indipendentemente dagli altri, può essere funzionante o guasto. Anche il sistema nel suo complesso può essere funzionante o guasto, a seconda degli stati delle componenti. La probabilità che il sistema funzioni è detta affidabilità del sistema. Negli esercizi seguenti, indichiamo con pi la probabilità che la componente i funzioni, per i = 1, 2, ..., n.
34. Commenta l'assunzione di indipendenza su sistemi reali, quali un'automobile o un computer.
35. Un sistema in serie
funziona se e solo se ciascuna componente funziona. Prova che l'affidabilità del sistema è
R = p1 p2 ··· pn.
36. Un sistema in parallelo
funziona se e solo se almeno una componente funziona. Prova che l'affidabilità del sistema è
R = 1 - (1 - p1)(1 - p2) ··· (1 - pn).
Più in generale, un sistema k di n funziona se e solo se almeno k delle n componenti funzionano. Nota che un sistema parallelo è un sistema 1 di n e un sistema in serie è un sistema n di n. Un sistema k di 2k + 1 è detto sistema a regola di maggioranza .
37. Considera un sistema di 3 componenti con affidabilità p1 = 0.8, p2 =
0.9, p3 = 0.7. Trova l'affidabilità di
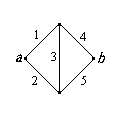
In certi casi, il sistema può essere rappresentato graficamente. I bordi rappresentano i componenti e i vertici le connessioni tra componenti. Il sistema funzione se e solo se c'è una strada percorribile tra i due vertici, che indicheremo con a e b.
38. Trova l'affidabilità della rete a ponte riportata sotto, in termini delle affidabilità delle componenti pi, i =
1, 2, 3, 4, 5. Suggerimento: un approccio può essere di condizionare al fatto che la componente 3 sia funzionante o guasta.
39. Un sistema è formato da 3 componenti collegate in parallelo. Sotto basse condizioni di sforzo, le componenti sono indipendenti e ciascuna ha affidabilità 0.9; sotto condizioni di sforzo medie, le componenti sono indipendenti con affidabilità 0.8 e sotto condizioni di sforzo elevato le componenti sono indipendenti con affidabilità 0.7. La probabilità che le condizioni di sforzo siano basse è 0.5, medie 0.3 ed elevate 0.2.
Richiama la discussione sui test diagnostici del paragrafo precedente. Abbiamo un evento A di un esperimento casuale il cui verificarsi oppure no non può essere etichettati da 1 a n. Sia Ti le'vento in cui il test i è positivo per A. I test sono indipendenti nel senso che:
Se A si verifica, allora T1, T2, ..., Tn sono indipendenti e il test i ha sensitività
ai = P(Ti | A).
Se A non si verifica, allora T1, T2, ..., Tn sono indipendenti e il test i ha specificità
bi = P(Tic | Ac).
Possiamo generare un nuovo test composto scegliendo una regola di decisione in funzione dei risultati dei test individuali. In altre parole, l'evento T in cui il test composto è positivo per A è funzione di T1, T2, ..., Tn. Le regole di decisione più comuni sono simili alle strutture di affidabilità che abbiamo presentato poc'anzi. Un caso particolare interessante si ha quando gli n test sono applicazioni indipendenti di un dato test semplice. In cui caso, gli ai e i bi sono gli stessi.
40.
Considera l'esperimento composto positivo per A se e solo se ciascuno degli n test è positivo per A. Prova che
T2
···
Tn. 41. Considera l'esperimento composto positivo per A se e solo se almeno uno degli n test è positivo per A. Prova che
T2
···
Tn. Più in generale, possiamo definire il test composto k di n che risulta positivo per A se e solo se almeno k test individuali sono positivi per A. Il test dell'esercizio 1 è n di n test, mentre il test dell'esercizio 2 è 1 di n. Il test k di 2k + 1 è il test a regola di maggioranza.
42.
Supponiamo che una donna creda di avere pari probabilità di essere incinta o non esserlo. Compra tre test di gravidanza identici con sensitività 0.95 e specificità 0.9. I test 1 e 3 sono positivi e il test 2 è negativo. Trova la probabilità che la donna sia incinta.
43.
Supponi di applicare 3 test indipendenti ed identici per un evento A ciascuno con sensitività a e specificità b. Trova la sensitività e la specificità dei test
44. In un processo, l'imputato è condannato se e solo se tutti e 6 i giurati lo ritengono colpevole. Assumiamo che, se l'imputato è realmente colpevole, i giurati votino colpevole, indipendentemente l'uno dall'altro, con probabilità 0.95, mentre, se l'imputato è innocente, che i giurati votino non colpevole, indipendentemente l'uno dall'altro, con probabilità 0.8. Supponiamo che l'80% degli imputati che arrivano al processo siano colpevoli.
La forma più comune di emofilia è dovuta a un difetto del cromosoma X (uno dei due cromosomi che determinano il sesso). Indichiamo con h l'allele difettoso, collegato all'emofilia, e con H il corrispondente allele normale. Le donne hanno due cromosomi X, e h è recessivo. Quindi, una donna con gene HH è normale; una donna con gene hH o Hh è portatrice sano; infine una donna con gene hh ha la malattia. L'uomo ha solo un cromosoma X (il suo ulteriore cromosoma, il cromosoma Y, non ha effetto sulla malattia). Un uomo con gene h è emofilico, mentre un uomo con gene H è sano. Gli esercizi seguenti analizzano le modalità di trasmissione della malattia.
45.
Supponi che la madre sia portatrice sana e il padre normale. Spiega perché, indipendentemente da figlio a figlio,
46.
Supponi che la madre sia normale e il padre malato. Spiega perché
47.
Supponi che la madre sia portatrice sana e il padre malato. Spiega perché, indipendentemente da figlio a figlio,
48.
Supponi che la madre sia emofiliaca e il padre normale. Spiega perché
49.
Supponi che sia padre che madre siano emofiliaci. Spiega perché ogni figlio è emofiliaco.
Da questi esercizi puoi notare che la trasmissione della malattia a una figlia femmina si può verificare solo se la madre è almeno portatrice sana e il padre malato. In popolazione ampie, questa combinazione di eventi è rara, per cui la malattia è rara nelle donne.
50. Supponi che una donna abbia inizialmente probabilità 1/2 di essere portatrice sana. Sapendo che ha 2 figli maschi sani,
Supponiamo di avere N + 1 monete, etichettate 0, 1, ..., N. La moneta i è testa con probabilità i / N per ogni i. In particolare, osserva che la moneta 0 è a due croci e la moneta N a due teste. L'esperimento consiste nello scegliere a caso una moneta (cosicché ciascuna moneta abbia uguale probabilità di essere scelta) e lanciarla ripetutamente.
51. Mostra che la probabilità che i primi n lanci siano teste è
pN,n = [1 / (N + 1)]
i
= 0, ..., N (i / N)n.
52. Mostra che la probabilità condizionata che il lancio n + 1 sia testa sapendo che i precedenti n lanci sono stati testa è
pN,n+1 / pN,n.
53. Interpreta pN,n
come somma approssimata dell'integrale di xn da 0 a
1 per provare che
pN,n 
1 / (n + 1) as N
.
54. Concludi che
pN,n+1 / pN,n
(n + 1) / (n
+ 2) as N .
La probabilità condizionata limite dell'esercizio precedente è detta regola della successione di Laplace, in onore di Simon Laplace. Questa regola è stata usata da Laplace e altri come principio generale per stimare la probabilità condizionata che un evento si verifichi per la n + 1 -esima volta, sapendo h si è verificato n volte in successione.
55. Supponi che un missile abbia superato con succeso 10 test successivi. Calcola la stima di Laplace della probabilità che l'undicesimo test abbia successo. Sembra avere senso?
56. Commenta la validità della regola di Laplace come principio generale.