Laboratorio virtuale > Giochi di fortuna > 1 2 3 [4] 5 6 7 8

4. Craps

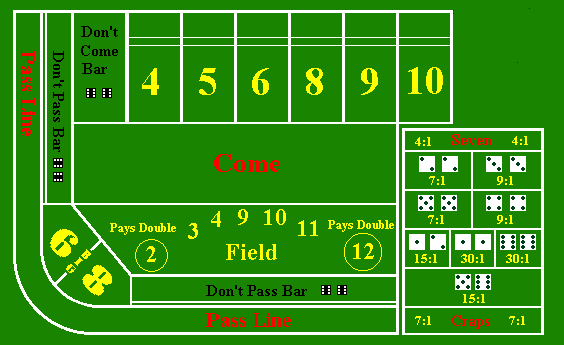
Craps è un gioco popolare nei casinò grazie alla sua complessità e alla ricca varietà di puntate che si possono fare. Una tavola da craps tipica è mostrata nella figura seguente:

Tavola da Craps

Secondo Richard Epstein, craps discende da un gioco precedente detto Hazard, che risale al medioevo. Le regole di Hazard vennero precisate formalmente da Montmort all'inizio del 1700. L'origine del nome craps è dubbia, ma può derivare dall'inglese crabs (granchi) o dal francese Crapeaud (rospo).

Dal punto di vista formale, craps è interessante perché costituisce un esempio di esperimento casuale in fasi distinte; l'evoluzione del gioco dipende dall'esito del primo lancio. In particolare, il numero di lanci è una variabile casuale.

Definizione del gioco

Le regole di craps sono le seguenti: il giocatore (detto tiratore) lancia due dadi equilibrati

  1. Se la somma è 7 o 11 al primo lancio, il tiratore ha vinto; tale evento è detto natural.
  2. Se la somma è 2, 3, o 12 al primo lancio, il tiratore ha perso; tale evento è detto craps.
  3. Se la somma è 4, 5, 6, 8, 9, o 10 al primo lancio, tale numero è il punteggio del tiratore. Il tiratore continua a tirare i dadi finché esce di nuovo il punteggio (nel qual caso vince) o esce 7 (nel qual caso perde).

Finché il giocatore vince o perde tirando craps, tiene i dadi e continua a tirare. Una volta che perde non riuscendo a fare il punteggio, si passano i dadi al tiratore seguente.

Consideriamo il gioco in termini più formali. L'assunzione di base è ovviamente che i dadi siano equilibrati e che gli esiti dei vari lanci siano indipendenti. Sia N il numero di lanci effettuato e sia (Xi, Yi) l'esito dell'i-esimo lancio per i = 1, 2, ..., N. Infine, sia Zi = Xi + Yi, la somma dei punteggi all'i-esimo lancio, e sia I la variabile indicatore della vittoria del giocatore.

Simulazione 1. Nell'applet craps, esegui un paio di volte l'esperimento e osservane gli esiti. Assicurati di aver capito bene le regole del gioco.

La probabilità di vittoria

Calcoliamo la probabilità che il tiratore vinca in più fasi, basandoci sull'esito del primo lancio.

Esercizio teorico 2. Prova che Z1 ha la funzione di densità di probabilità riportata nella tabella seguente:

z 2 3 4 5 6 7 8 9 10 11 12
P(Z1 = z) 1 / 36 2 / 36 3 / 36 4 / 36 5 / 36 6 / 36 5 / 36 4 / 36 3 / 36 2 / 31 1 / 36

La probabilità che il giocatore tiri il punteggio può essere calcolata utilizzando il condizionamento. Per esempio, supponiamo che il giocatore tiri un 4, per cui 4 è il punteggio. Il giocatore continua a tirare finché non esce un 4 o un 7. Il lancio finale è quindi uno dei seguenti:

(1, 3), (2, 2), (3, 1), (1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1).

Poiché i dadi sono equilibrati, i risultati sono equiprobabili, pertanto la probabilità che il giocatore faccia il punteggio 4 è 3 / 9). Un'argomento simile può essere utilizzato per gli altri punti. I risultati sono presentati nell'esercizio seguente.

Esercizio teorico 3. Prova che la probabilità di fare il punteggio z sono quelle riportate nella tabella seguente:

z 4 5 6 8 9 10
P(I = 1 | Z1 = z) 3 / 9 4 / 10 5 / 11 5 / 11 4 / 10 3 / 9

Esercizio teorico 4. Usa i risultati degli esercizi 1 e 3 per mostrare che

  1. P(I = 1) = 244 / 495 ~ 0.49292
  2. P(I = 0) = 251 / 495 ~ 0.50707

Notiamo che craps è un gioco quasi equilibrato.

Puntate

Nel gioco del craps vi è un'incredibile varietà di puntate. Negli esercizi seguenti presenteremo alcune puntate tipiche e calcoleremo le loro densità, media e deviazione standard. (La maggior parte di tali puntate sono evidenziate nella figura del tavolo da craps presentata sopra). Notiamo, in ogni caso, che alcuni dei dettagli delle puntate e in particolare gli odds variano da casinò a casinò. Ovviamente il valore atteso di ogni puntata è inevitabilmente negativo (per il giocatore), per cui il giocatore è destinato a perdere, nel lungo termine. Tuttavia, come vedremo, alcune puntate sono migliori di altre.

Una puntata pass punta sul fatto che il tiratore vinca e paga 1:1.

Esercizio teorico 5. Sia W la vincita di una puntata pass unitaria. Mostra che

  1. P(W = -1) = 251 / 495, P(W = 1) = 244 / 495.
  2. E(W) = -0.0141.
  3. sd(W) = 0.9999.

Simulazione 6. Nell'applet craps, seleziona la puntata pass. Simula 1000 replicazioni, aggiornando ogni 10, e osserva la convergenza della densità empirica e dei momenti di W ai loro valori teorici. Supponi di puntare 1$ per ogni replicazione. A quanto ammonterebbe la tua vincita netta?

Una puntata don't pass punta sul fatto che il tiratore perda, a parte il fatto che il 12 al primo lancio è escluso (cioè, il tiratore perde, ma chi ha puntato su don't pass non vince né perde). Tale è il significato della frase don't pass bar double 6 sul tavolo da craps. Anche la puntata don't pass paga 1:1.

Esercizio teorico 7. Sia W la vincita di una puntata don't pass unitaria. Mostra che

  1. P(W = -1) = 244 / 495, P(W = 0) = 1 / 36, P(W = 1) = 949 / 1980.
  2. E(W) = -0.01363.
  3. sd(W) = 0.9859.

Simulazione 8. Nell'applet craps, seleziona la puntata don't pass. Simula 1000 replicazioni, aggiornando ogni 10, e osserva la convergenza della densità empirica e dei momenti di W ai loro valori teorici. Supponi di puntare 1$ per ogni replicazione. A quanto ammonterebbe la tua vincita netta?

Le puntate come e don't come sono analoghe a pass e don't pass, ma vengono fatte dopo aver stabilito il punteggio.

Una puntata field è relativa all'esito del tiro successivo. Paga 1:1 se esce 3, 4, 9, 10, o 11, 2:1 se esce 2 o 12 e perde altrimenti.

Esercizio teorico 9. Sia W la vincita di una puntata field unitaria. Mostra che

  1. P(W = -1) = 5 / 9, P(W = 1) = 7 / 18, P(W = 2) = 1 / 18.
  2. E(W) = -0.0556
  3. sd(W) = 1.0787

Simulazione 10. Nell'applet craps, seleziona la puntata field. Simula 1000 replicazioni, aggiornando ogni 10, e osserva la convergenza della densità empirica e dei momenti di W ai loro valori teorici. Supponi di puntare 1$ per ogni replicazione. A quanto ammonterebbe la tua vincita netta?

Una puntata 7 è relativa all'esito del lancio successivo. Paga 4:1 se esce un 7 e perde altrimenti. Similmente, una puntata 11 paga 15:1 se esce 11. Nonostante la cabalistica del numero 7, mostreremo nel prossimo esercizio che la puntata 7 è una delle peggiori.

Esercizio teorico 11. Sia W la vincita di una puntata 7 unitaria. Mostra che

  1. P(W = -1) = 5 / 6, P(W = 4) = 1 / 6.
  2. E(W) = -0.1667.
  3. sd(W) = 1.8634.

Simulazione 12. Nell'applet craps, seleziona la puntata 7. Simula 1000 replicazioni, aggiornando ogni 10, e osserva la convergenza della densità empirica e dei momenti di W ai loro valori teorici. Supponi di puntare 1$ per ogni replicazione. A quanto ammonterebbe la tua vincita netta?

Esercizio teorico 13. Sia W la vincita di una puntata 11 unitaria. Mostra che

  1. P(W = -1) = 17 / 18, P(W = 15) = 1 / 18.
  2. E(W) = -0.1111
  3. sd(W) = 3.6650;

Simulazione 14. Nell'applet craps, seleziona la puntata 11. Simula 1000 replicazioni, aggiornando ogni 10, e osserva la convergenza della densità empirica e dei momenti di W ai loro valori teorici. Supponi di puntare 1$ per ogni replicazione. A quanto ammonterebbe la tua vincita netta?

Tutte le puntate craps sono relative al tiro successivo. Pagano 7:1 se esce 2, 3 o 12 e perdono altrimenti. Similmente, la craps 12 paga 30:1 se esce un 12 e perde altrimenti. Infine, la craps 3 paga 15:1 se esce 3 e perde altrimenti

Esercizio teorico 15. Sia W la vincita di una puntata craps unitaria. Mostra che

  1. P(W = -1) = 8 / 9, P(W = 7) = 1 / 9.
  2. E(W) = -0.1111.
  3. sd(W) = 2.5142

Simulazione 16. Nell'applet craps, seleziona la puntata craps. Simula 1000 replicazioni, aggiornando ogni 10, e osserva la convergenza della densità empirica e dei momenti di W ai loro valori teorici. Supponi di puntare 1$ per ogni replicazione. A quanto ammonterebbe la tua vincita netta?

Esercizio teorico 17. Sia W la vincita di una puntata craps 2 o craps 12 unitaria. Mostra che

  1. P(W = -1) = 35 / 36, P(W = 30) = 1 / 36.
  2. E(W) = -0.1389.
  3. sd(W) = 5.0944.

Simulazione 18. Nell'applet craps, seleziona la puntata craps 2. Simula 1000 replicazioni, aggiornando ogni 10, e osserva la convergenza della densità empirica e dei momenti di W ai loro valori teorici. Supponi di puntare 1$ per ogni replicazione. A quanto ammonterebbe la tua vincita netta?

Simulazione 19. Nell'applet craps, seleziona la puntata craps 12. Simula 1000 replicazioni, aggiornando ogni 10, e osserva la convergenza della densità empirica e dei momenti di W ai loro valori teorici. Supponi di puntare 1$ per ogni replicazione. A quanto ammonterebbe la tua vincita netta?

Esercizio teorico 20. Sia W la vincita di una puntata craps 3 unitaria. Mostra che

  1. P(W = -1) = 17 / 18, P(W = 15) = 1 / 18.
  2. E(W) = -0.1111
  3. sd(W) = 3.6650.

Simulazione 21. Nell'applet craps, seleziona la puntata craps 3. Simula 1000 replicazioni, aggiornando ogni 10, e osserva la convergenza della densità empirica e dei momenti di W ai loro valori teorici. Supponi di puntare 1$ per ogni replicazione. A quanto ammonterebbe la tua vincita netta?

La puntata big 6 scommette che 6 esca prima di 7. Similmente, la puntata big 8 scommette che 8 esca prima di 7. Entrambe pagano alla pari (1:1).

Esercizio teorico 22. Sia W la vincita di una puntata big 6 o big 8 unitaria. Mostra che

  1. P(W = -1) = 6 / 11, P(W = 1) = 5 / 11.
  2. E(W) = -0.0909
  3. sd(W) = 0.9959

Simulazione 23. Nell'applet craps, seleziona la puntata big 6. Simula 1000 replicazioni, aggiornando ogni 10, e osserva la convergenza della densità empirica e dei momenti di W ai loro valori teorici. Supponi di puntare 1$ per ogni replicazione. A quanto ammonterebbe la tua vincita netta?

Simulazione 24. Nell'applet craps, seleziona la puntata big 8. Simula 1000 replicazioni, aggiornando ogni 10, e osserva la convergenza della densità empirica e dei momenti di W ai loro valori teorici. Supponi di puntare 1$ per ogni replicazione. A quanto ammonterebbe la tua vincita netta?

Una puntata hardway può essere fatta sui numeri 4, 6, 8 o 10. Scommette che il numero scelto n esca "a metà" cioè (n / 2, n / 2), prima che esca 7 e prima che il numero scelto esca in qualche altra combinazione. Le puntate sul 4 e sul 10 pagano 7:1 e quelle sul 6 e l'8 9:1.

Esercizio teorico 25. Sia W la vincita di una puntata hardway 4 o hardway 10 unitaria. Mostra che

  1. P(W = -1) = 8 / 9, P(W = 7) = 1 / 9.
  2. E(W) = -0.1111.
  3. sd(W) = 2.5142

Simulazione 26. Nell'applet craps, seleziona la puntata hardway 4. Simula 1000 replicazioni, aggiornando ogni 10, e osserva la convergenza della densità empirica e dei momenti di W ai loro valori teorici. Supponi di puntare 1$ per ogni replicazione. A quanto ammonterebbe la tua vincita netta?

Simulazione 27. Nell'applet craps, seleziona la puntata hardway 10. Simula 1000 replicazioni, aggiornando ogni 10, e osserva la convergenza della densità empirica e dei momenti di W ai loro valori teorici. Supponi di puntare 1$ per ogni replicazione. A quanto ammonterebbe la tua vincita netta?

Esercizio teorico 28. Sia W la vincita di una puntata hardway 6 o hardway 8 unitaria. Mostra che

  1. P(W = -1) = 10 / 11, P(W = 9) = 1 / 11.
  2. E(W) = -0.0909
  3. sd(W) = 2.8748

Simulazione 29. Nell'applet craps, seleziona la puntata hardway 6. Simula 1000 replicazioni, aggiornando ogni 10, e osserva la convergenza della densità empirica e dei momenti di W ai loro valori teorici. Supponi di puntare 1$ per ogni replicazione. A quanto ammonterebbe la tua vincita netta?

Simulazione 30. Nell'applet craps, seleziona la puntata hardway 8. Simula 1000 replicazioni, aggiornando ogni 10, e osserva la convergenza della densità empirica e dei momenti di W ai loro valori teorici. Supponi di puntare 1$ per ogni replicazione. A quanto ammonterebbe la tua vincita netta?

La distribuzione del numero di lanci

Calcoliamo ora la distribuzione e i momenti del numero di lanci N in una partita di craps. Tale variabile casuale non è di interesse particolare per il casinò o i giocatori, ma costituisce un buon esercizio. Per definizione, se il tiratore vince o perde al primo tiro, N = 1. Altrimenti il tiratore continua finché non fa il punteggio o tira 7. In quest'ultimo caso, possiamo utilizzare la distribuzione geometrica, che indica il numero di prova a cui si verifica il primo successo in una sequenza di prove Bernoulliane.

Esercizio teorico 31. Mostra che P(N = 1 | Z1 = z) = 1 if z = 2, 3, 7, 11, 12.

Esercizio teorico 32. Mostra che P(N = n | Z1 = z) = p(1 - p)n - 2 per n = 2, 3, 4, ... per i valori di z e p indicati nella tabella seguente. La distribuzione condizionata di N - 1 dato Z1 = z è quindi geometrica con parametro p.

z 4 5 6 8 9 10
p 9 / 36 10 / 36 11 / 36 11 / 36 10 / 36 9 / 36

La distribuzione di N è una mistura.

Esercizio teorico 33. Usa il risultato dell'esercizio precedente per mostrare che

  1. P(N = 1) = 12 / 36.
  2. P(N = n) = (1 / 24)(3 / 4)n - 2 + (5 / 81)(13 / 18)n - 2 + (55 / 648)(25 / 36)n - 2 per n = 2, 3, ...

Esercizio teorico 34. Semplifica numericamente per trovare i primi valori della funzione di densità di probabilità di N:

n 1 2 3 4 5
P(N = n) 0.33333 0.18827 0.13477 0.09657 0.06926

Esercizio teorico 35. Trova la probabilità che il gioco duri più di 8 lanci.

Esercizio teorico 36. Usa il condizionamento e i momenti della distribuzione geometrica per mostrare che

  1. E(N) = 3.3758
  2. E(N2) = 15.0013.
  3. var(N) = 3.6056.
  4. sd(N) = 1.8988.

Laboratorio virtuale > Giochi di fortuna > 1 2 3 [4] 5 6 7 8
Sommario | Applets | Dati | Biografie | Risorse | Indice analitico | ©