Laboratorio virtuale > Valore atteso > 1 2 3 [4] 5 6 7

4. Funzioni generatrici

Al solito, iniziamo con l'introdurre un esperimento casuale definito su un certo sapazio campionario e con misura di probabilità P. Una funzione generatrice di una variabile casuale è il valore atteso di una certa trasformazione della variabile. Tutte le funzioni generatrici posseggono tre importanti proprietà:

  1. Sotto condizioni blande, la funzione generatrice individua completamente la distribuzione.
  2. La funzione generatrice della somma di variabili indipendenti è il prodotto delle funzioni generatrici.
  3. I momenti della variabile casuale possono essere ottenuti a partire dalle derivate della funzione generatrice.

La proprietà 2 è usata di frequente per determinare la distribuzione di una somma di variabili indipendenti. Al contrario, ricordiamo che la funzione di densità di probabilità di una somma di variabili indipendenti è la convoluzione delle funzioni di densità individuali, operazione molto più complessa.

La funzione generatrice di probabilità

Supponiamo che N sia una variabile casuale a valori in {0, 1, 2, ...}. La funzione generatrice di probabilità G di N è definita come

G(t) = E(tN).

Sia f la funzione di densità di probabilità di N, cosicché f(n) = P(N = n) per n = 0, 1, 2, ... Gli esercizi seguenti individuano le proprietà principali.

Esercizio teorico 1. Prova che G(t) = sommatorian = 0, 1, ... f(n) tn.

G(t) è quindi una serie di potenze in t, coi valori della funzione di densità di probabilità che fanno da coefficienti. Ricorda che, sulla base dei risultati di analisi, esiste un r tale che la serie converge assolutamente per |t| < r e diverge per |t| > r. Il numero r è detto raggio di convergenza della serie.

Esercizio teorico 2. Prova che G(1) = 1 e quindi r >= 1.

Ricorda, dall'analisi, che una serie di potenze può essere derivata termine a termine, esattamente come un polinomio. Ciascuna serie di derivate ha lo stesso raggio di convergenza della serie originale.

Esercizio teorico 3. Prova che f(n) = G(n)(0)/n! per n = 0, 1, 2, ...

Dall'esercizio 3, nota che G individua completamente la distribuzione di N.

Esercizio teorico 4. Mostra che P(N è pari) = [1 + G(-1)] / 2.

Esercizio teorico 5. Sia r > 1. Dimostra che G(k)(1) = E[(N)k] dove

(N)k = N(N - 1) ··· (N - k + 1).

I momenti dell'esercizio 5 si dicono momenti fattoriali.

Esercizio teorico 6. Mostra che var(N) = G(2)(1) + G(1)(1) - [G(1)(1)]2.

Esercizio teorico 7. Supponi che N1 e N2 siano indipendenti e con funzione generatrice di probabilità rispettivamente G1 e G2. Dimostra che la funzione generatrice di probabilità di N1 + N2 è

G(t) = G1(t)G2(t).

Esercizio teorico 8. Supponi che I sia una variabile indicatore con P(I = 1) = p. Mostra che

G(t) = 1 - p + pt per ogni t.

Esercizio teorico 9. Supponi che N abbia funzione di densità P(N = k) = C(n, k) pk (1 - p)n-k, per k = 0, 1, ..., n. dove n appartenente a {1, 2, ...} e p appartenente a (0, 1) sono parametri. Si ha allora una distribuzione binomiale con parametri n e p. Dimostra che

  1. G(t) = (1 - p + pt)n.
  2. E(N) = np
  3. var(N) = np(1 - p)
  4. P(N è pari) = [1 + (1 - 2p)n] / 2

Esercizio teorico 10. Usa i risultati dei due esercizi precedenti per mostrare che, se I1, I2, ... In sono variabili indicatore indipendenti con parametro p, allora N = I1 + I2 + ··· + In ha distribuzione binomiale con parametri n e p.

Esercizio teorico 11. Supponi che N abbia funzione di densità P(N = n) = (1 - p)n-1 p per n = 1, 2, ... dove p appartenente a (0, 1) è un parametrro. Si tratta della distribuzione geometrica con parametro p. Prova che

  1. G(t) = tp / [1 - t(1 - p)] for t < 1 / (1 - p).
  2. E(N) = 1 / p.
  3. var(N) = (1 - p) / p2.
  4. P(N è pari) = (1 - p) / (2 - p).

Esercizio teorico 12. Supponi che N abbia funzione di densità P(N = n) = e-a an / n! per n = 0, 1, 2, ..., dove a > 0 è un parametrro. Si tratta della distribuzione di Poisson con parametro a. Mostra che

  1. G(t) = exp[a(t - 1)] for any t.
  2. E(N) = a
  3. var(N) = a
  4. P(N è pari) = [1 + exp(-2a)] / 2.

La funzione generatrice dei momenti

Sia X una variabile casuale a valori in un sottinsieme di R. La funzione generatrice dei momenti di X è la funzione M definita da

M(t) = E[exp(tX)] for t R.

Nota che, poiché exp(tX) è una variabile casuale non negativa, M(t) esiste, come numero reale o infinito positivo, per ogni t.

La funzione generatrice dei momenti possiede molte delle proprietà della funzione generatrice di probabilità, ma è definita per un insieme più ampio di variabili casuali. Le proprietà fondamentali, che assumiamo senza dimostrarle, sono le seguenti: se M(t) è finita per t in un intervallo aperto J attorno a 0, allora

  1. M individua completamente la distribuzione di X.
  2. M ha derivate di ogni ordine in J e M(n)(t) = E[Xn exp(tX)] per t appartenente a J.

Negli esercizi seguenti, assumi che le funzioni generatrici dei momenti siano finite in un intorno di 0.

Esercizio teorico 13. Prova che M(n)(0) = E(Xn) per ogni intero non negativo n.

Pertanto le derivate della funzione generatrice dei momenti in 0 determinano i momenti della variabile (di qui il nome).

Esercizio teorico 14. Supponi che X sia una variabile casuale con funzione generatrice dei momenti M e che a e b siano costanti. Dimostra che la funzione generatrice dei momenti di aX + b è

R(t) = exp(bt) M(at).

Esercizio teorico 15. Supponi che X1 e X2 siano variabili casuali indipendenti, con funzioni generatrici dei momenti M1 e M2. Prova che la funzione generatrice dei momenti di X1 + X2 è

M(t) = M1(t) M2(t).

Esercizio teorico 16. Supponi che N sia una variabile casuale a valori in {0, 1, 2, ...}, con funzione generatrice di probabilità G. Prova che la funzione generatrice dei momenti di N is

M(t) = G(et).

Esercizio teorico 17. Supponi che X abbia distribuzione uniforme su (a, b). Mostra che

  1. M(t) = [exp(tb) - exp(ta)] / [t(b - a)] se t <> 0; M(0) = 1.
  2. E(Xn) = (bn + 1 - an + 1) / [(n + 1)(b - a)]

Esercizio teorico 18. Supponi che X abbia funzione di densità f(x) = r exp(-rx) per x > 0, dove r > 0 è un parametro (ciò individua la distribuzione esponenziale con parametro di velocità r). Prova che

  1. M(t) = r / (r - t) per t < r.
  2. E(Xn) = n! / rn.

Esercizio teorico 19. Supponi che Z abbia funzione di densità f(z) = exp(-z2 / 2) / (2 pi)1/2 per z appartenente a R. Si tratta quindi di una distribuzione normale standardizzata. Prova che

  1. M(t) = exp(t2 / 2) per t appartenente a R.
  2. E(Z2n) = (2n)! / [n!2n] per n = 0, 1, ...
  3. E(Z2n + 1) = 0 per n = 0, 1, ...

L'esercizio seguente riporta esempi di distribuzioni per le quali la funzione generatrice dei momenti è infinita.

Esercizio teorico 20. Supponi che X abbia densità f(x) = a / xa + 1 per x > 1, dove a > 0 è un parametro. Si tratta della distribuzione di Pareto con parametro di forma a.

  1. Mostra che M(t) = infinito per ogni t > 0 e a > 0.
  2. Prova che E(Xn) < infinito se e solo se a > n.

Controesempi

Nell'ultimo esercizio abbiamo considerato una distribuzione per la quale solo alcuni dei momenti sono finiti; ovviamente, la funzione generatrice dei momenti era infinita. In questa sezione, riportiamo un esempio di una distribuzione per la quale tutti i momenti sono finiti, ma la funzione generatrice dei momenti è comunque infinita. Inoltre, vedremo due distribuzioni distinti che hanno i momenti di tutti gli ordini uguali.

Supponi che Z abbia distribuzione normale standardizzata, e sia X = exp(Z). La distribuzione di X è detta lognormale.

Esercizio teorico 21. Usa la formula del cambiamento di variabile per dimostrare che X ha funzione di densità

f(x) = exp[-ln2(x) / 2] / [(2 pi)1/2 x] per x > 0.

Esercizio teorico 22. Usa la funzione generatrice dei momenti della distribuzione normale standardizzata per mostrare che X ha momenti di ogni ordine finiti

E(Xn) = exp(n2 / 2) per n = 1, 2, ...

Esercizio teorico 23. Dimostra che la funzione generatrice dei momenti di X è infinita per ogni numero positivo:

E[exp(tX)] = infinito per t > 0.

Esercizio teorico 24. Sia g(x) = f(x) {1 + sin[2 pi ln(x)]} per x > 0. Prova che g è una funzione di densità di probabilità.

Esercizio teorico 25. Poni che Y abbia funzione di densità g nell'esercizio precedente. Prova che Y ha gli stessi momenti di X:

E(Yn) = exp(n2 / 2) for n = 1, 2, ...

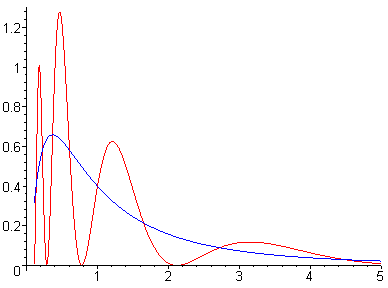
I grafici di f e g sono riportati qui sotto, rispettivamente in blu e rosso.

Densità di due distribuzioni con gli stessi momenti

I limiti di Chernoff

Esercizio teorico 26. Supponi che X sia una variabile casuale con funzione generatrice dei momenti M. Prova i limiti di Chernoff:

  1. P(X >= x) <= exp(-tx) M(t) per ogni t > 0
  2. P(X <= x) <= exp(-tx) M(t) per ogni t < 0

Suggerimento: Mostra che P(X >= x) = P[exp(tX) >= exp(tx)] se t > 0 e P(X <= x) = P[exp(tX) >= exp(tx)] se t < 0. Poi usa la disuguaglianza di Markov.

Ovviamente, il miglior limite di Chernoff (in (a) o (b)) si ottiene trovando il t che minimizza exp(-tx) M(t).

Esercizio teorico 27. Supponi che N abbia distribuzione di Poisson con parametro a > 0. Usa i limiti di Chernoff per provare che, se n > a, allora

P(N >= n) <= exp(n - a) (a / n)n.

La funzione generatrice dei momenti congiunta

Supponiamo ora che (X1, X2) sia un vettore casuale relativo a un esperimento, a valori in un sottinsieme di R2. La funzione generatrice dei momenti (congiunta) di (X1, X2) è definita come

M(s, t) = E[exp(sX1 + tX2)] per s, t R.

Di nuovo, una cosa importante da notare è che se la funzione generatrice dei momenti è finita in un rettangolo aperto contenente (0, 0), allora tale funzione individua completamente la distribuzione di (X1, X2).

Siano M1, M2 e M+ la funzione generatrice dei momenti rispettivamente di X1, X2, and X1 + X2.

Esercizio teorico 28. Prova che M(s, 0) = M1(s)

Esercizio teorico 29. Prova che M(0, t) = M2( t)

Esercizio teorico 30. Prova che M(t, t) = M+(t)

Esercizio teorico 31. Prova che X1 e X2 sono indipendenti se e solo se

M(s, t) = M1(s) M2( t) per (s, t) in un rettangolo attorno a (0, 0).

Ovviamente tali risultati hanno omologhi nel caso multivariato generale. Solo la notazione si fa più complessa.

Esercizio teorico 32. Supponi che (X, Y) sia distribuito uniformemente sul triangolo {(x, y): 0 < x < y < 1}.

  1. Trova la funzione generatrice dei momenti congiunta.
  2. Trova la funzione generatrice dei momenti di X.
  3. Trova la funzione generatrice dei momenti di Y.
  4. Trova la funzione generatrice dei momenti di X + Y.

Esercizio teorico 33. Supponi che (X, Y) abbia funzione di densità f(x, y) = x + y per 0 < x < 1, 0 < y < 1.

  1. Trova la funzione generatrice dei momenti congiunta.
  2. Trova la funzione generatrice dei momenti di X.
  3. Trova la funzione generatrice dei momenti di Y.
  4. Trova la funzione generatrice dei momenti di X + Y.

Laboratorio virtuale > Valore atteso > 1 2 3 [4] 5 6 7
Sommario | Applets | Dati | Biografie | Risorse | Indice analitico | ©