Laboratorio virtuale > Distribuzioni notevoli > 1 2 3 4 5 6 7 8 [9] 10 11 12 13 14 15 15
Introdurremo in questo paragrafo una famiglia di distribuzioni a due parametri di particolare importanza in probabilitÓ e statistica.
La funzione beta B(a, b) Ŕ definita per a > 0 e b > 0 come
B(a, b) = ![]() (0,
1) ua - 1(1 - u)b-1 du.
(0,
1) ua - 1(1 - u)b-1 du.
![]() 1. Mostra che B(a,
b) Ŕ finita per a > 0 e b > 0 percorrendo i seguenti passi:
1. Mostra che B(a,
b) Ŕ finita per a > 0 e b > 0 percorrendo i seguenti passi:
![]() 2. Mostra che
2. Mostra che
![]() 3. Dimostra che la funzione beta pu˛ essere scritta in termini della funzione gamma come segue:
3. Dimostra che la funzione beta pu˛ essere scritta in termini della funzione gamma come segue:
B(a, b) = gam(a) gam(b) / gam(a + b).
Suggerimento: Esprimi gam(a + b) B(a, b) come integrale doppio rispetto a x e y, con x > 0 e 0 < y < 1. Usa la trasformazione w = xy, z = x - xy e il teorema del cambiamento di variabile per integrali multipli. Tale trasformazione Ŕ una funzione biiettiva da (x, y) su z > 0, w > 0; il Jacobiano della trasformazione inversa vale 1 / (z + w). Mostra che l'integrale trasformato vale gam(a) gam(b).
![]() 4. Mostra che, se j e k sono interi positivi, allora
4. Mostra che, se j e k sono interi positivi, allora
B(j, k) = (j - 1)!(k - 1)! / (j + k -1)!.
![]() 5. Mostrare che B(a
+ 1, b) = [a / (a + b)] B(a, b).
5. Mostrare che B(a
+ 1, b) = [a / (a + b)] B(a, b).
![]() 6. Si mostri che B(1/2,
1/2) =
6. Si mostri che B(1/2,
1/2) = ![]() .
.
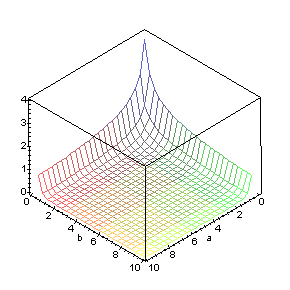
Riportiamo qui sotto un grafico di B(a, b) sulla regione 0 < a < 10, 0 < b < 10.
![]() 7. Mostra che f
Ŕ una funzione di densitÓ di probabilitÓ per ogni a
> 0 e b > 0:
7. Mostra che f
Ŕ una funzione di densitÓ di probabilitÓ per ogni a
> 0 e b > 0:
f(u) = ua - 1 (1 - u)b - 1 / B(a, b), 0 < u < 1.
una distribuzione con questa densitÓ Ŕ detta distribuzione beta con parametri a e b. La distribuzione beta Ŕ utile per modellare probabilitÓ e proporzioni, in particolare in ambito Bayesiano. Pur possedendo solo due paraemtri, questa distribuzione contempla una ricca varietÓ di forme:
![]() 8. Disegna il grafico della funzione di densitÓ beta. Osserva le differenze qualitative nella forma della funzione di densitÓ nei seguenti casi:
8. Disegna il grafico della funzione di densitÓ beta. Osserva le differenze qualitative nella forma della funzione di densitÓ nei seguenti casi:
![]() 9. Nell'appletvariabile casuale, seleziona la distribuzione beta. Poni i parametri a ciascuna delle combinazioni proposte nell'esercizio 1. In ognuno di questi casi, osserva la forma della funzione di densitÓ e simula 1000 replicazioni con frequenza di aggiornamento di 10. Osserva la convergenza della funzione di densitÓ empirica a quella teorica.
9. Nell'appletvariabile casuale, seleziona la distribuzione beta. Poni i parametri a ciascuna delle combinazioni proposte nell'esercizio 1. In ognuno di questi casi, osserva la forma della funzione di densitÓ e simula 1000 replicazioni con frequenza di aggiornamento di 10. Osserva la convergenza della funzione di densitÓ empirica a quella teorica.
In alcuni casi particolari, la funzione di ripartizione e la funzione quantile possono essere espresse in forma chiusa.
![]() 10.
Per a > 0 e b = 1, mostra che
10.
Per a > 0 e b = 1, mostra che
![]() 11.
Per a = 1 e b > 0, dimostrare che
11.
Per a = 1 e b > 0, dimostrare che
In generale sussiste un'interessante relazione tra le funzioni di ripartizione beta e la distribuzione binomiale.
![]() 12. Sia n dato.
Sia Fp la funzione di ripartizione di una binomiale con parametri n e p e sia Gk la funzione di ripartizione di una beta con parametri n - k + 1 e k. Si dimostri che
12. Sia n dato.
Sia Fp la funzione di ripartizione di una binomiale con parametri n e p e sia Gk la funzione di ripartizione di una beta con parametri n - k + 1 e k. Si dimostri che
Fp(k - 1) = Gk(1 - p).
Suggerimento: Si esprima Gk(1 - p) come integrale della funzione di densitÓ della distribuzione beta e si integri per parti.
![]() 13. Nell'applet quantile, seleziona la distribuzione beta. Modifica i parametri e osserva la forma delle funzioni di densitÓ e di ripartizione. In ognuno dei seguenti casi, trova mediana, primo e terzo quartile e scarto interquartile. Disegna il boxplot
13. Nell'applet quantile, seleziona la distribuzione beta. Modifica i parametri e osserva la forma delle funzioni di densitÓ e di ripartizione. In ognuno dei seguenti casi, trova mediana, primo e terzo quartile e scarto interquartile. Disegna il boxplot
I momenti della distribuzione beta sono esprimibili facilmente in termini della funzione beta.
![]() 14. Supponi che U
abbia distribuzione beta con parametri a e b. Dimostra che
14. Supponi che U
abbia distribuzione beta con parametri a e b. Dimostra che
E(Uk) = B(a + k, b) / B(a, b).
![]() 15. Supponi che U
abbia distribuzione beta con parametri a e b. Dimostra che
15. Supponi che U
abbia distribuzione beta con parametri a e b. Dimostra che
![]() 16. Nell'appletvariabile casuale, seleziona la distribuzione beta. Poni i parametri a ciascuna delle combinazioni proposte nell'esercizio 1. In ognuno di questi casi, osserva la forma della barra media/deviazione standard e simula 1000 replicazioni con frequenza di aggiornamento di 10. Osserva la convergenza dei momenti empirici a quelli teorici.
16. Nell'appletvariabile casuale, seleziona la distribuzione beta. Poni i parametri a ciascuna delle combinazioni proposte nell'esercizio 1. In ognuno di questi casi, osserva la forma della barra media/deviazione standard e simula 1000 replicazioni con frequenza di aggiornamento di 10. Osserva la convergenza dei momenti empirici a quelli teorici.
![]() 17. Si supponga che X
abbia distribuzione gamma con parametri a e r,
che Y abbia distribuzione gamma con parametri b e r e
che X e Y siano indipendenti. Si mostri che
U = X / (X + Y) ha distribuzione beta con parametri a e b.
17. Si supponga che X
abbia distribuzione gamma con parametri a e r,
che Y abbia distribuzione gamma con parametri b e r e
che X e Y siano indipendenti. Si mostri che
U = X / (X + Y) ha distribuzione beta con parametri a e b.
![]() 18. Supponi che U
abbia distribuzione beta con parametri a e b. Mostra che
1 - U ha distribuzione beta con parametri b e a.
18. Supponi che U
abbia distribuzione beta con parametri a e b. Mostra che
1 - U ha distribuzione beta con parametri b e a.
![]() 19. Supponi che X
abbia distribuzione F con m gradi di libertÓ al numeratore e n gradi di libertÓ al denominatore. Dimostra che
19. Supponi che X
abbia distribuzione F con m gradi di libertÓ al numeratore e n gradi di libertÓ al denominatore. Dimostra che
U = (m / n)X / [1 + (m / n)X]
ha distribuzione beta con parametri a = m / 2 e b = n / 2.
![]() 20. Supponiamo che X
abbia distribuzione beta con parametri a > 0 e b > 0. Mostra che tale distribuzione Ŕ una famiglia esponenziale a due parametri
con parametri naturali a - 1 e b - 1, e statistiche naturali ln(X) e ln(1 - X).
20. Supponiamo che X
abbia distribuzione beta con parametri a > 0 e b > 0. Mostra che tale distribuzione Ŕ una famiglia esponenziale a due parametri
con parametri naturali a - 1 e b - 1, e statistiche naturali ln(X) e ln(1 - X).
La distribuzione beta Ŕ inoltre la distribuzione delle statistiche d'ordine di un campione casuale estratto da una distribuzione uniforme.