{s:
s > 0} sk - 1exp(-s)ds.Laboratorio virtuale > Distribuzioni notevoli > 1 2 [3] 4 5 6 7 8 9 10 11 12 13 14 15
In questo paragrafo studieremo una famiglia di distribuzioni che ricopre particolare importanza nel calcolo delle probabilità. In particolare i tempi di arrivo nei processi di Poisson hanno distribuzione gamma, e la distribuzione chi-quadro è un caso speciale della gamma.
La funzione gamma è definita per k > 0 da
gam(k) = {s:
s > 0} sk - 1exp(-s)ds.
1. Mostrare che l'integrale che definisce la funzione gamma converge per ogni k > 0.
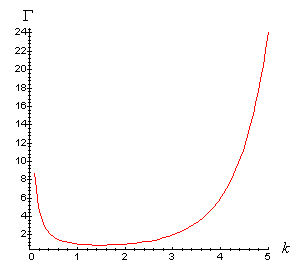
Riportiamo qui sotto il grafico della funzione gamma sull'intervallo (0, 5):
2. Integrare per parti e mostrare che per ogni k > 0,
gam(k + 1) = k gam(k).
3. Usa il risultato dell'esercizio precedente per mostrare che se k è un intero positivo, allora
gam(k) = (k - 1)!.
4. Usa la funzione di densità normale standardizzata per mostrare che
gam(1/2) = 
1/2.
5. Mostrare che la seguente funzione è funzione di densità di probabilità per ogni k > 0:
f(x) = xk - 1exp(-x) / gam(k) per x > 0.
Una variabile casuale X che possiede questa funzione di densità ha distribuzione gamma con parametro di forma k. L'esercizio seguente mostra che questa famiglia ha una ricca varietà di forme grafiche, e fa capire perché k si chiama parametro di forma.
6. Disegna la funzione di densità di probabilità della distribuzione gamma in ognuno dei seguenti casi:
7. Nell'applet variabile casuale, seleziona la distribuzione gamma. Modifica il parametro di forma e osserva la forma della funzione di densità. Poni k = 3, e replica la simulazione 1000 volte, con frequenza di aggiornamento di 10, e osserva la convergenza della funzione di densità empirica a quella teorica.
8. Supponiamo che la durata di un certo apparecchio (in unità di 100 ore) abbia distribuzione gamma con k
= 3. Trova la probabilità che l'apparecchio duri più di 300 ore.
La funzione di ripartizione e la funzione quantile non posseggono forme chiuse e semplici. Valori approssimati di queste funzioni si possono ottenere tramite l' applet quantile.
9. Utilizzando l'
applet quantile, trova la mediana, il primo e il terzo quartile e lo scarto interquartile in ciascuno dei casi seguenti:
Il seguente esercizio dà la media e la varianza della distribuzione gamma.
10. Sia X
gamma-distribuita con parametro di forma k.
Si dimostri che
In generale, i momenti possono essere espressi facilmente in termini della funzione gamma:
11.
Si abbia X con distribuzione gamma con parametro di forma k.
Si dimostri che
L'esercizio seguente individua la funzione generatrice dei momenti.
12. Supponi che X
abbia distribuzione gamma con parametro di forma k. Mostra che
E[exp(tX)] = 1 / (1 - t)k per t < 1.
13. Nella simulazione variabile casuale, seleziona la distribuzione gamma. Modifica il parametro di forma e osserva la dimensione e la posizione della barra media/deviazione standard. Poni k
= 4, e simula 1000 replicazioni con frequenza di aggiornamento 10 e osserva la convergenza dei momenti empirici ai momenti teorici.
14. Immagina che la lunghezza dei petali di un certo tipo di fiore (in cm) abbia distribuzione gamma con k = 4. Trova la media e la deviazione standard della lunghezza dei petali.
Spesso la distribuzione gamma viene generalizzata aggiungendo un parametro di scala. Pertanto, se Z possiede distribuzione gamma semplice con parametro di forma k, come definita sopra, allora per b > 0, X = bZ ha distribuzione gamma con parametro di forma k e parametro di scala b. Il reciproco del parametro di scala è noto come parametro di velocità, specie nel contesto del processo di Poisson. La distribuzione gamma con parametri k = 1 e b è detta distribuzione esponenziale con parametro di scala b (o parametro di velocità r = 1 / b).
Risultati analoghi a quelli presentati poc'anzi seguono da semplici proprietà della trasformazione di scala.
15.
Sia X gamma-distribuita con parametro di forma k
e parametro di scala b. Si mostri che X ha funzione di densità
f(x) = xk - 1 exp(-x / b) / [gam(k)bk] per x > 0.
Si ricordi che l'aggiunta di un parametro di scala non modifica la forma della distribuzione, ma semplicemente dimensiona il grafico orizzontalmente e verticalmente. In particolare, si hanno le stesse forme elementari presentate nell'esercizio 6.
16.
Sia X gamma-distribuita con parametro di forma k
e parametro di scala b. Mostra che, se k > 1, la moda è a
(k - 1)b.
17.
Sia X gamma-distribuita con parametro di forma k
e parametro di scala b. Mostra che
18.
Sia X gamma-distribuita con parametro di forma k
e parametro di scala b. Mostra che,
19.
Sia X gamma-distribuita con parametro di forma k
e parametro di scala b. Mostra che,
E[exp(tX)] = 1 / (1 - bt)k per t < 1 / b.
20. Nell'applet variabile casuale, seleziona la distribuzione gamma. Modifica i parametri e osserva la dimensione e la posizione della barra media/deviazione standard. Poni k
= 4 e b = 2, e simula 1000 replicazioni con frequenza di aggiornamento 10 e osserva la convergenza dei momenti empirici ai momenti teorici.
21. Supponi che la durata di un certo congegno (in ore) abbia distribuzione gamma con parametro di forma k
= 4 e parametro di scala b = 100.
La prima trasformazione che presentiamo è semplicemente una ridefinizione del significato del parametro di scala.
22. Supponi che
X abbia distribuzione gamma con parametro di forma k e parametro di scala b. Mostra che, se c > 0 allora cX ha distribuzione gamma con parametro di forma k e parametro di scala bc.
Si noti che, se il parametro di scala è fisso, la famiglia gamma è chiusa rispetto alla somma di variabili indipendenti.
23. Supporre che X1
abbia distribuzione gamma con paraemtro di forma k1 e parametro di scala b;
che X2 abbia distribuzione gamma con paraemtro di forma k2
e parametro di scala b; e che X1 e X2 siano
indipendenti. Dimostrare che X1 + X2
ha distribuzione gamma con parametro di forma k1 + k2
e parametro di scala b. Suggerimento: Usare le funzioni generatrici dei momenti.
24. Supponi che X
abbia distribuzione gamma con parametro di forma k > 0 e parametro di scala b
> 0. Mostra che tale distribuzione è una famiglia esponenziale a due parametri con parametri naturali k - 1 e 1 / b,
e statistiche naturali X e ln(X).
Dall'esercizio precedente si deduce che, se Y ha distribuzione gamma con paramero di forma intero k ae parametro di scala b, allora
Y = X1 + X2 + ··· + Xk
dove X1, X2, ..., Xk sono indipendenti e distribuite esponenzialmente con parametro b. Segue dal teorema limite centrale che se k è grande (e non necessariamente intero), la distribuzione gamma può essere approssimata dalla normale con media kb e varianza kb2. Più precisamente, la distribuzione della variabile standardizzata riportata qui sotto converge alla normale standardizzata per k che tende a infinito:
(Y - kb) / (kb)1/2.
25. Nell'applet variabile casuale, seleziona la distribuzione gamma. Modifica k
e b e osserva la forma della funzione di densità. Poni k = 10 e b
= 2, e simula 1000 replicazioni con frequenza di aggiornamneto pari a 10 e osserva la convergenza della funzione di densità empirica a quella teorica.
26. Supponi che Y
abbia distribuzione gamma con parametri k = 10 e b = 2. Trova le approssimazioni della normale a:
Laboratorio virtuale > Distribuzioni notevoli > 1 2
[3]
4 5 6 7 8 9 10 11
12 13
14 15
Sommario | Applets
| Dati | Biografie
| Risorse
| Indice analitico | ©